
- SAP Community
- Products and Technology
- Technology
- Technology Blogs by SAP
- Understand accuracy measure of time series forecas...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Last revision date: September 5th, 2023
When I wrote the blog Time Series Forecasting in SAP Analytics Cloud Smart Predict in Detail, I mentioned that the accuracy of predictive forecasting models is calculated by an indicator named Expected Mean Absolute Percentage Error (Expected MAPE*). The goal of this blog is to lift the veil on the following aspects of this indicator.
- Why we have used this one?
- Understand its definition.
- How is Expected MAPE calculated?
Since the QRC of Q3-2023, four new indicators are now exposed and explained in section New indicators. The user has now the choice to use the one(s) with which he/she is the more comfortable.
Let’s start with an example
The time series measures the production of coffee (in kilograms) by month from January 2011 to December 2020. The goal is to forecast the production in the next twelve months. In SAP Analytics Cloud (SAC) Predictive Planning, we create a predictive scenario set as shown in figure below.

Figure 1: Predictive Model
If we go to the Explanation tab, we notice that this predictive model was built incrementally by smoothing the time series with more weight given to recent observations as shown in Figure 2.
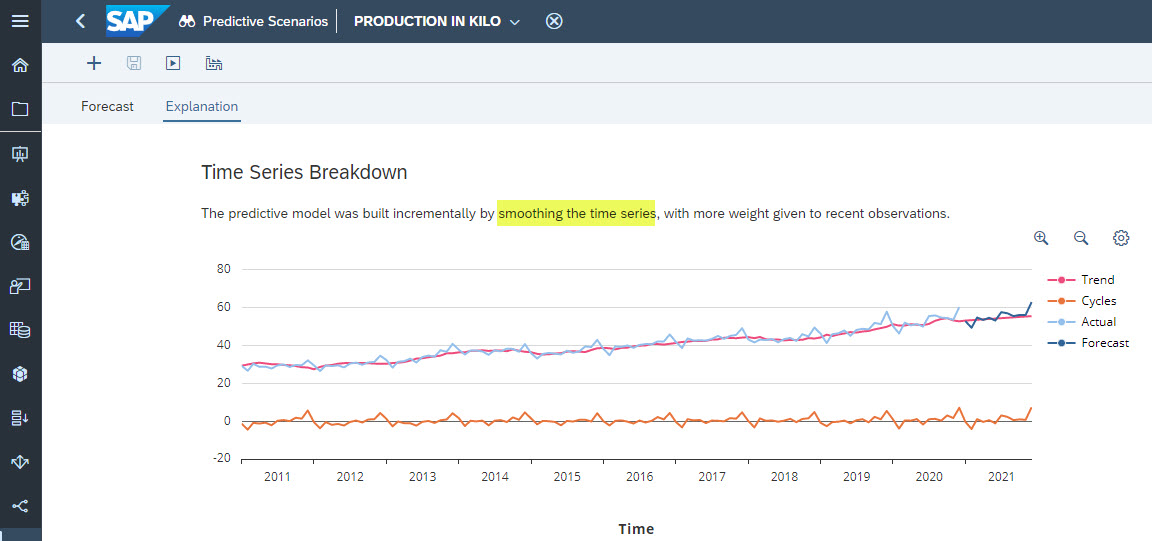
Figure 2: Explanation of the Predictive Model
At the top of Figure 1, we can read that the Expected MAPE is 3.54%. This indicator corresponds to the average error made by the predictive model over the requested horizon. It is used to determine the accuracy of a model. The lower this indicator is, the better the predictive model is.
The Expected MAPE:
- Captures the performance of the predictive model with a horizon of several periods (12 months in our example)
- Is computed based on the forecasts generated with a validation dataset, which contains data which has not been used to train the predictive model. Doing so enables us to estimate the performance of the predictive model when applied on unseen data.
- Is calculated based on the average performance obtained at each sub horizon of the requested horizon.
But how is it computed? The name Mean Absolute Percentage Error says it all. The first information in the name is that a percentage error is calculated. This is the error done by the predictive model. The second information is provided by the letter ‘M’. It is the mean of the percentage errors over the number of forecasted periods2. In the example, we want to forecast the production of coffee for the twelve next months. The percentage errors for each of these months is the difference between the predictive forecast and the actual value divided by this actual value. Then the average between these twelve percentage errors is computed.
Lift the veil
The problem is that in real life, these errors cannot be calculated because for the periods in the future, the actual values
To estimate the performance of the predictive model, SAC Smart Predict/Predictive Planning computes an expected MAPE. It measures performances based on forecasts generated with only the known data at the forecast date. As a result, the expected MAPE does not solve the problem of needing future values to compute performance. It gives an estimation of the performance we would obtain when we strictly use only known values to compute forecasts.
The expected MAPE is computed from the data of the validation dataset of the time series. The validation dataset corresponds to the most recent 25% of the historical data as shown in Figure 3. SAC Smart Predict/Predictive Planning assumes that the time series behaves the same way on the most recent dates as well as future dates (horizon). As a consequence, it also assumes that the predictive model will make comparable prediction errors on both periods.

Figure 3: Training and Validation datasets
When SAC Smart Predict/Predictive Planning creates time series forecasting models, it computes the predictive forecasts for all values of the horizon and for all data points of the validation dataset. These predictive forecasts are used to execute the different steps needed to compute the Expected MAPE. Figure 4 below shows a table that stores the predictive forecasts at all dates and for all values of the horizon. This table is used internally to compute the Expected MAPE.
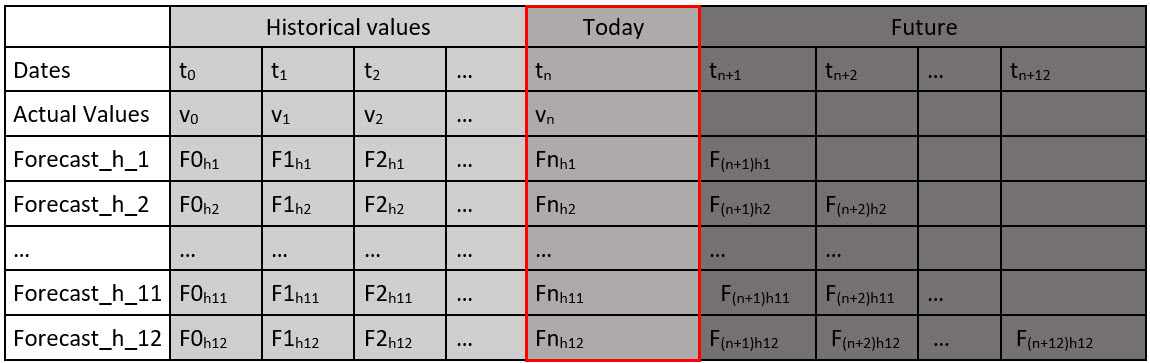
Figure 4: Actuals and forecasts on all the range of the horizon
How to interpret this table? The column in the red rectangle is read like this: Today at time tn;
- The actual value is vn.
- Fnh1 is the forecasts horizon 1 generated for this date. In other words, it is the forecast generated at date tn-1 to predict the value of the series at date tn.
- Fnh2 is the forecasts horizon 2 generated for this date. In other words, it is the forecast generated at date tn-2 to predict the value of the series at date tn.
- …
- Fnh12 is the forecasts horizon 12 generated for this date. In other words, it is the forecast generated at date tn-12 to predict the value of the series at date tn.
Figure 5 below shows the part of the table with the forecasts made at each horizon for each date of the future periods.
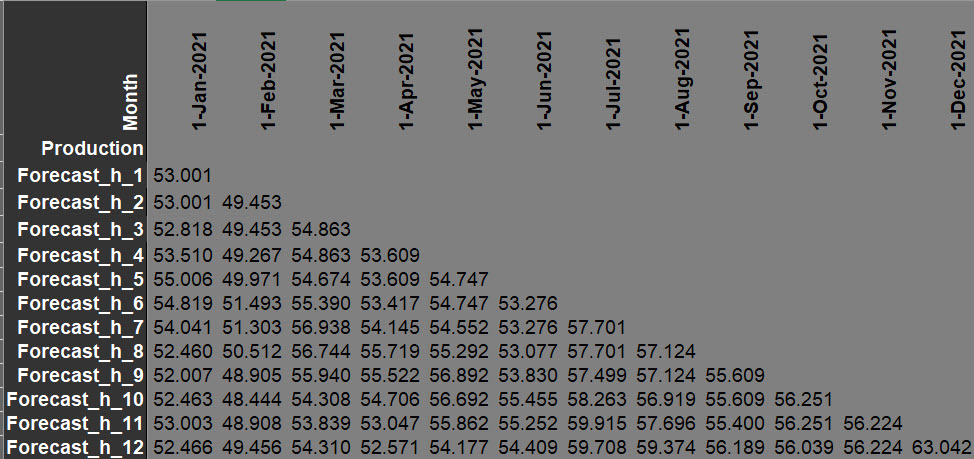
Figure 5: Predictions for the future months
The variable to predict, ‘Production’ is of course unknown for the future months. To compute the Expected MAPE, we use the validation dataset as shown in figure 6 below.

Figure 6: Predictions on the validation dataset (zoom on last values)
For November 2020:
- The prediction at horizon 1 is 55.107 (blue rectangle). This prediction was computed one month ago from data until October 2020.
- The prediction at horizon 3 is 56.552 (green rectangle). This prediction was computed three months ago from data until August 2020.
We see that in November the predicted value at horizon 1 done in October (blue rectangle), is different from the prediction at horizon 3 done in August 2020 (green rectangle). This happens when the predictive model is either an auto-regressive model or a lag model or an exponential smoothing model, which is the case for this example. When the predictive model relies solely on time (for example a linear trend with a monthly seasonality), the prediction at hx is equivalent to the prediction at h1 x-1 months later.” In such a case, in our example, predictions in green and blue rectangles will have been the same.
There are 120 months of historical data. This means that the validation dataset contains 30 months (25% of the data) as shown in figure 7.

Figure 7: Predictions on the validation dataset
Compute the Absolute Percentage Errors (APEs)
The APE (Absolute Percentage Error) at a given time t is the absolute value of the difference between the predicted value at this time for a given horizon and the actual value at this time divided by the actual value at this time.
APE(t, h) = ABSOLUTE ((Forecast(t, h) – Actual(t))/Actual(t))
Let us look at the internally computed table: The header is the date of each event. The first row Production is the actual value of the target to predict. The rows Forecast_h_i (for i = 1 to 12) are the forecasts generated at date t-1, t-2, ... t-h to predict the value at date t.
For November 2020, the actual value is 53.688 while the predictive model predicts for this month Forecast_h_1 = 55.107. At a horizon of 2 months, the prediction is Forecast_h_2 = 55.107, and so on until Forecast_h_12 = 55.400.
This means that it is possible to compare predictions with actuals and get the error of the predictions.
For example, for November 2020
APE(November 2020, Forecast_h_1) = ABSOLUTE((55.107 – 53.688) / 53.688) = 0.0264
APE(November 2020, Forecast_h_2) = ABSOLUTE((55.107 – 53.688) / 53.688) =0.0264
APE(November 2020, Forecast_h_3) = ABSOLUTE((56.552 – 53.688) / 53.688) =0.0533
And for Dec 2020
APE(Dec 2020, Forecast_h_1) = ABSOLUTE((60.041 – 60.422) / 60.422) = 0.0063
APE(Dec 2020, Forecast_h_2) = ABSOLUTE((60.041 – 60.422) / 60.422) =0.0063
APE(Dec 2020, Forecast_h_3) = ABSOLUTE((60.721 – 60.422) / 60.422) =0.0049
Figure 8 below gives all the APEs for the entire range of the horizon (at the end of the document, you will find a link to an Excel file with all formulas).

Figure 8: Computation of all APEs for all data points of the validation dataset and all horizons
Compute the Mean Absolute Percentage Error (MAPE) for each horizon
There is not only one MAPE, but one per range of the horizon. The MAPE for a given horizon is the mean of all the APEs.
MAPE (h) = AVERAGE(APE(ti, h)) for all dates of the validation dataset
For example, row in green rectangle in figure 8, MAPE (h = 1) = AVERAGE (APE of row APE_h_1) = 0.023782
Row in brown rectangle in figure 8, MAPE (h = 3) = AVERAGE (APE of row APE_h_3) = 0.024770
Compute the Expected Mean Absolute Percentage Error (Expected MAPE)
The Expected MAPE is simply the mean of all the previously MAPE indicators calculated for each horizon. In our example, it is the sum of the MAPEs divided by the horizon.
Expected MAPE (horizon) = SUM(MAPEi)/horizon for i = 1 to horizon
In our example
Expected MAPE (12) = ( 0.023782 +
0.023782 +
0.024770 +
0.025890 +
0.029966 +
0.031375 +
0.034735 +
0.038467 +
0.041411 +
0.045452 +
0.051101 +
0.053512) / 12 = 0.035353
SAC Smart Predict/Predictive Planning round this indicator to 3.54%
New indicators
Since the quarterly release of Q3 2023, there are four additional performance indicators in the predictive model.
- Expected Mean Absolute Error (Expected MAE)
- Expected Mean Absolute Scaled Error (Expected MASE)
- Expected Root Mean Squared Error (Expected RMSE)
- Expected R-squared (Expected R²)

Figure 9: Expected MAPE and new indicators
They are well-known indicators that because they use them during their activities, and they can compare more easily the performance of SAC Smart Predict predictive models with others.
Expected Mean Absolute Error (Expected MAE)
MAE is a measure of errors between paired observations expressing the same phenomenon. MAE is the mean of absolute error. The error is the difference between the predicted value and the actual value. Figure 10 illustrates the computation of the absolute errors.
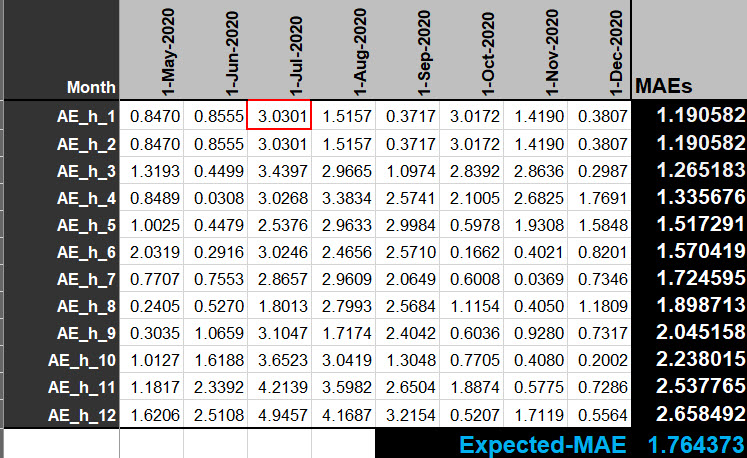
Figure 10: The value in the red rectangle is the absolute value of the difference the actual value in July 2020 and the predicted value for h1
The MAE at a given horizon is the average of all the absolute errors at this horizon. A MAE is calculated for each value of the horizon. In our example, the horizon is equal to 12. Thus, there will be 12 MAE computed from the data of the validation dataset as shown in figure 10.
At the end, we obtain an Expected MAE which is the average of the 12 MAE.
The formula to compute an MAE for horizon hi is:
MAE(hi) = 1/n * SUM(ABS(Vj - Fihi)) where j = 1 to n
where n is the number of values in the validation dataset.
Expected Mean Absolute Scaled Error (Expected MASE)
When we want to compare the performance of predictive models on several time series which are not at the same scale, the MAE is not a good measure because its value grows with the scale. To correct this scaling problem, we prefer to use the MASE instead of the MAE. The formula is:
MASE = MAE / Scaling Factor
The scaling factor is based on a Lag 1 computed between the absolute difference of the actual values at time ti and ti-1. These differences are computed on all the values of the training dataset as shown in figure 11. The scaling factor is the average of these absolute differences.

Figure 11: Computation of the Scaling Factor
Now that we have the Scaling Factor, we can compute for each horizon the corresponding MASE with the MAE of figure 10. The Expected MASE is the average of the 12 MASE as shown in figure 12.
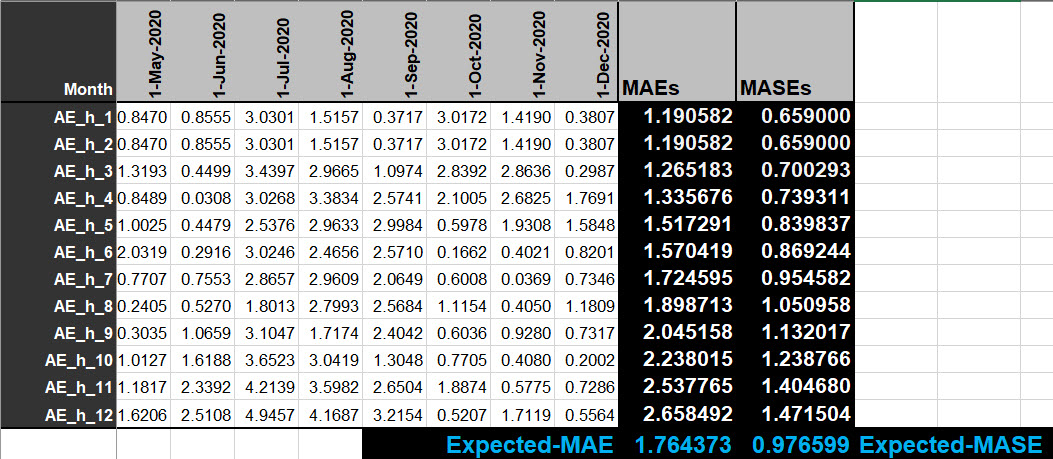
Figure 12: MASE for each horizon and Expected MASE
Expected Root Mean Squared Error (Expected RMSE)
RMSE is mean quadratic error. It measures the average magnitude of the error. It’s the square root of the average of squared differences between prediction and actual observation. The formula of the RMSE at a given horizon is:

Cells at figure 13 gives the square of the differences between actual values and forecasted values for all horizons. The last column contains the square root of the average of these squared differences. Finally, the Expected RMSE is the average of the 12 RMSEs.

Figure 13: Computation of the RMSE
Comparison between MAE and RMSE
Both MAE and RMSE express average model prediction error in units of the target variable. Both metrics can range from 0 to and are indifferent to the direction of errors. They are negatively oriented scores, which means lower values are better.
RMSE gives a relatively high weight to large errors since the errors are squared before they are averaged. This means the RMSE should be more useful when large errors are particularly undesirable.
RMSE tends to be increasingly larger than MAE as the size validation dataset increases.
RMSE has the benefit of penalizing large errors more. In consequence, it can be more appropriate in cases. RMSE is more sensitive to error outlier with high value.
From an interpretation standpoint, MAE is clearly the winner. RMSE does not describe average error alone and has other implications that are more difficult to tease out and understand.
Expected R-squared (Expected R2)
R2 is a statistical measure that represents the proportion of the variance for the target variable that is explained by an independent variable or variables in a regression model. R2 explains to what extent the variance of one variable explains the variance of the second variable.
An R2 of 100% means that the variations of the target variable are completely explained by variations of the independent variables.
An R2 of 50%, tells that approximately half of the observed variation can be explained by the model's inputs.
An R2 of 0% tells that the variations of the target variable are not explained by the model’s inputs.
R2 is computed on the validation dataset and its formula is:

Where n is the size of the validation dataset.
![]() is the average of the actual values on the validation dataset.
is the average of the actual values on the validation dataset.
Figure 14 shows the steps to compute R2. Expected R2 is the average of the 12 R2.

Figure 14: Computation of expected R2
Minimize influence of extreme values
What is the problem exactly? When Predictive scenario is defined with one or several entities, several predictive models are built: one for each valid combination of the values of the entities. Each of these predictive models have a performance indicator as shown in figure 15.
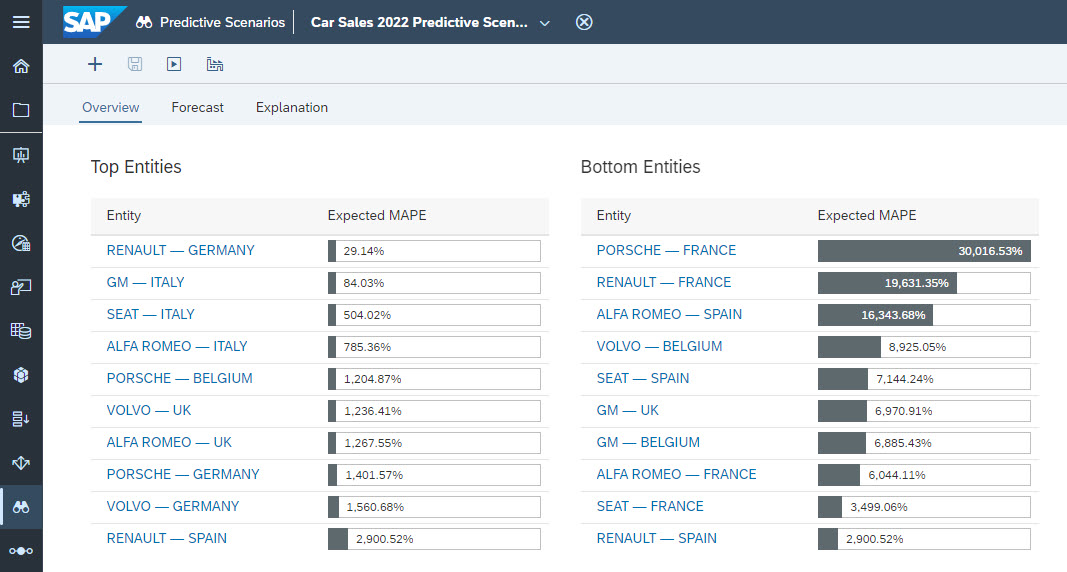
Figure 15: Expected MAPE of the predictive models built on entities Brand and Country
In this example, we see that the Expected MAPE for the predictive models ‘RENAULT - GERMANY’ or ‘GM – ITALY’ are good while the one for ‘PORSCHE – FRANCE’ and ‘RENAULT – FRANCE’ are very bad. The extreme bad values have an influence on the overall Expected MAPE because it is an average of individual expected MAPE. This can lead the customer to think that the predictions are in general not accurate. In fact, this is not the reality because good predictive models are affected by the poor result of few predictive models.
To avoid this situation, we have added three new ways to compute the global performance indicator in addition to the average. This new information is visible inside the status panel at the bottom or in the Overview page as shown in figure 16.

Figure 16: New Global Performance Indicators presentation
The Median discard extreme values from the result so that it is not impacted.
The 3rd Quartile is the middle value between the median and the highest value (maximum) of the data set. It is known as the upper quartile, as 75% of the data lies below this point.
Conclusion
At the end of this blog, I hope that the veil is lifted on why we have these accuracy indicators as well as on the way they are calculated . The product focuses on what is important for the user and automates more of the process to get insights, to get forecasts inside your planning models and to justify them.
I also hope these explanations increase your confidence in the product. If you appreciated reading this blog, I would be grateful if you would like it. You might want to comment on it as well. Thank you.
Resources
- Time Series Forecasting in SAP Analytics Cloud Smart Predict in Detail
- SAC Smart Predict – What goes on under the hood
- Mean absolute percentage error
Files that will be available for download
In GitHub (https://github.com/antoinechabert/predictive), you will find two Excel files:
- The dataset I use in this blog: PRODUCTION_IN_KILO.xlsx
- A worksheet with all the steps of the computation of the Expected-MAPE (with the Excel formula included) and the new indicators: Statistical Indicator Computations.xlsx
Notes:
*: Expected MAPE was named Horizon-Wide MAPE in earlier versions of SAC Smart Predict/Predictive Planning, but it is the same indicator.
**: In earlier versions, the number of forecasted periods was called the horizon.
- SAP Managed Tags:
- SAP Analytics Cloud,
- SAP Analytics Cloud, augmented analytics
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
-
ABAP CDS Views - CDC (Change Data Capture)
2 -
AI
1 -
Analyze Workload Data
1 -
BTP
1 -
Business and IT Integration
2 -
Business application stu
1 -
Business Technology Platform
1 -
Business Trends
1,661 -
Business Trends
86 -
CAP
1 -
cf
1 -
Cloud Foundry
1 -
Confluent
1 -
Customer COE Basics and Fundamentals
1 -
Customer COE Latest and Greatest
3 -
Customer Data Browser app
1 -
Data Analysis Tool
1 -
data migration
1 -
data transfer
1 -
Datasphere
2 -
Event Information
1,400 -
Event Information
64 -
Expert
1 -
Expert Insights
178 -
Expert Insights
270 -
General
1 -
Google cloud
1 -
Google Next'24
1 -
Kafka
1 -
Life at SAP
784 -
Life at SAP
11 -
Migrate your Data App
1 -
MTA
1 -
Network Performance Analysis
1 -
NodeJS
1 -
PDF
1 -
POC
1 -
Product Updates
4,578 -
Product Updates
323 -
Replication Flow
1 -
RisewithSAP
1 -
SAP BTP
1 -
SAP BTP Cloud Foundry
1 -
SAP Cloud ALM
1 -
SAP Cloud Application Programming Model
1 -
SAP Datasphere
2 -
SAP S4HANA Cloud
1 -
SAP S4HANA Migration Cockpit
1 -
Technology Updates
6,886 -
Technology Updates
395 -
Workload Fluctuations
1
- Harnessing the Power of SAP HANA Cloud Vector Engine for Context-Aware LLM Architecture in Technology Blogs by SAP
- UNVEILING THE INNOVATIONS OF ARTIFICIAL INTELLIGENCE in Technology Q&A
- Forecast Local Explanation with Automated Predictive (APL) in Technology Blogs by SAP
- SAP Datasphere - Space, Data Integration, and Data Modeling Best Practices in Technology Blogs by SAP
- New Partner Content on SAP Business Accelerator Hub (Q1 ’24) in Technology Blogs by SAP
| User | Count |
|---|---|
| 11 | |
| 10 | |
| 10 | |
| 9 | |
| 8 | |
| 7 | |
| 7 | |
| 7 | |
| 7 | |
| 6 |