
- SAP Community
- Products and Technology
- Technology
- Technology Blogs by Members
- Solving the Knight's Tour Problem with HANA Graph
Technology Blogs by Members
Explore a vibrant mix of technical expertise, industry insights, and tech buzz in member blogs covering SAP products, technology, and events. Get in the mix!
Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
former_member19
Active Participant
Options
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
10-29-2018
6:21 AM
Last week during a Code Jam at TechEd Barcelona, vitaliy.rudnytskiy threw the glove at me by starting a challenge to solve the "Knight's Tour" problem using the Graph capabilities of HANA.
The problem is best summarised as the following: "find a succession of moves of a knight piece on a chess board such that the knight visits each square exactly once".

We can model the chess board like a graph with the squares as the vertices and all the possible moves as the edges.
By using this abstraction, the problem actually boils down to a special case of the more general Hamiltonian Path problem, which is basically the search of a path traversing all vertices of a graph exactly once.

HANA has built-in support for processing graphs. As of now, it has the following main features:
To solve this problem, I used the stored procedures together with the graph representation.
The first step would be to generate the chess board as a graph. We will label the rows from 1 to 8 and the columns from A to H:

To store the graph, I defined the data model as follows:
I did not want to manually define the board, so I wrote a procedure for generating it for me based on an input size:
After creating the procedure, I was able to simply call it to fill my tables:
WebIDE has a built-in graph viewer which provides a pretty nice visualisation of the chess board:

Lastly, I defined a table type for representing paths:
The first idea that came to my mind was to try to solve it via backtracking. I decided to not do it, because of the fact that it would be simply too slow.
Vanilla backtracking has an exponential asymptotic time complexity. In our graph each node has potentially 8 neighbours and we have to find a 64-node long path, so it would need to do (slightly less than) 8 ^ 64 steps to finish the whole algorithm.
Of course, if we would stop when we find the first solution it will be faster, but I still decided that there must be a better solution.
After thinking on it a while, I decided that it should be possible to find a solution using a greedy algorithm with an appropriate selection heuristic.
The first heuristic that I tried was to always try to go towards the bottom of the board and slowly fill in from there. After fighting a little with the GraphScript language, I wrote the following procedure:
Unfortunately, this approach failed miserably, yielding mediocre results:

The problem looked to me like once the bottom half of the board was almost full, the knight got into a dead end. To prevent this, I tried applying a different heuristic: to always go as close as possible to the center of the board.
I envisioned that the knight will spin around the center of the board. What I did not realise is that this approach would basically cut off the corners of the board leading the knight to be stuck in one of the corners:
Seeing that my heuristics are not working, I decided to read a little literature on the topic.
Source: Squirrel, Douglas, and Paul Çull. "A Warnsdorff-Rule Algorithm for Knight's Tours." (1996).
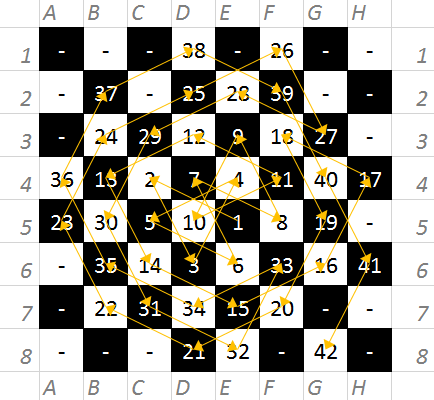
After reading some papers, I found out that I was very close to a correct solution. The heuristic that I was searching for was to always select the next node to be the one with the smallest degree. That is, we select the node which has the smallest amount of not-yet-visited neighbours.
Basically, this would yield the exact opposite result as the image above: first visit the margins of the board, then the center:

I finally got a solution! But what I don't like at this heuristic is the fact that, when we have to decide on the next node and there are two nodes with the exact same score, we always take the first one. In the literature they usually take one at random, but there is no RANDOM function in GraphScript.
Sometimes this heuristic may not be able to yield a result (although I never encountered this situation), so I wanted to improve it further.
Source: Pohl, Ira. "A method for finding Hamilton paths and Knight's tours." (1967).
One possible way of breaking ties would be to repeatedly apply the selection mechanism on the candidate nodes. Because I cannot really write a recursive call using GraphScript, I decided to go for a single level tie-breaking:
Running it seems to generate the expected result:

I still don't like this solution, because even for asymmetrical arrangements, we still have to take a random choice (due to the lack of recursion).
Source: Ganzfried, Sam. "A Simple Algorithm for Knight’s Tours." (2004).
Another idea for the tie breaking is to select from the candidate nodes based on the distance from the center of the board (take the node with the maximal distance to the center):
Surprisingly, running this for the same starting point generated the same result as Pohl's tie-breaking (most of the time).
I don't want to give a false impression and make people think that everything went smoothly. I actually encountered a few bugs and limitations which made me waste a few hours of my time:
Overall, I think that working with the Graph Engine is fun, but it is still not a fully mature technology. Actually, this might apply to the whole XSA and not only to the Graph capabilities. Coming from the Java ecosystem, where you can have an excellent developer experience, developing on HANA using the WebIDE is somewhat lacklustre.
The problem is best summarised as the following: "find a succession of moves of a knight piece on a chess board such that the knight visits each square exactly once".

Graph Theory
We can model the chess board like a graph with the squares as the vertices and all the possible moves as the edges.
By using this abstraction, the problem actually boils down to a special case of the more general Hamiltonian Path problem, which is basically the search of a path traversing all vertices of a graph exactly once.

Graph Engine
HANA has built-in support for processing graphs. As of now, it has the following main features:
- Storing and representing graphs (basically you need a vertex and an edge table and then you can create a so-called "workspace" out of them).
- Running some simple algorithms on graphs (neighbourhood, shortest path, connected components, etc).
- Performing queries based on the openCypher query language.
- Writing stored procedures using a dedicated GraphScript language.
To solve this problem, I used the stored procedures together with the graph representation.
Chess Board
The first step would be to generate the chess board as a graph. We will label the rows from 1 to 8 and the columns from A to H:

To store the graph, I defined the data model as follows:
CREATE TABLE nodes (
label VARCHAR(2),
row_number INT NOT NULL,
col_number INT NOT NULL,
PRIMARY KEY (label)
);
CREATE TABLE edges(
label VARCHAR(5) NOT NULL,
from_node VARCHAR(2) NOT NULL,
to_node VARCHAR(2) NOT NULL,
PRIMARY KEY (label)
);
CREATE GRAPH WORKSPACE board
EDGE TABLE edges SOURCE COLUMN from_node
TARGET COLUMN to_node KEY COLUMN label
VERTEX TABLE nodes KEY COLUMN label;I did not want to manually define the board, so I wrote a procedure for generating it for me based on an input size:
CREATE OR REPLACE PROCEDURE generate_board_for_knights(
IN size INT,
OUT nodes TABLE(
label VARCHAR(2),
row_number INT,
col_number INT
),
OUT edges TABLE(
label VARCHAR(5),
from_node VARCHAR(2),
to_node VARCHAR(2)
)
) LANGUAGE SQLSCRIPT READS SQL DATA AS BEGIN
nodes = SELECT col_label || row_label AS label,
row_number, col_number
FROM (
-- generate row numbers from 1 to 8
SELECT GENERATED_PERIOD_START AS row_number,
TO_VARCHAR(GENERATED_PERIOD_START) AS row_label
FROM SERIES_GENERATE_INTEGER(1, 1, 9)
) AS row_table
CROSS JOIN (
-- generate column numbers from 1 to 8
-- and column labels from A to H
SELECT GENERATED_PERIOD_START AS col_number,
NCHAR(ASCII('A') + GENERATED_PERIOD_START - 1) AS col_label
FROM SERIES_GENERATE_INTEGER(1, 1, 9)
) AS col_table;
-- the edge label is simply the node labels
-- joined by a hyphen (e.g. A1-C2)
edges = SELECT A.label || '-' || B.label AS label,
A.label AS from_node, B.label AS to_node
FROM :nodes AS A CROSS JOIN :nodes AS B
WHERE (ABS(A.row_number - B.row_number) = 2
AND ABS(A.col_number - B.col_number) = 1)
OR (ABS(A.row_number - B.row_number) = 1
AND ABS(A.col_number - B.col_number) = 2);
END;After creating the procedure, I was able to simply call it to fill my tables:
CALL "GENERATE_BOARD_FOR_KNIGHTS"(8, nodes, edges) WITH OVERVIEW;WebIDE has a built-in graph viewer which provides a pretty nice visualisation of the chess board:

Lastly, I defined a table type for representing paths:
CREATE TYPE tt_path AS TABLE(label VARCHAR(2));Naive Approach
The first idea that came to my mind was to try to solve it via backtracking. I decided to not do it, because of the fact that it would be simply too slow.
Vanilla backtracking has an exponential asymptotic time complexity. In our graph each node has potentially 8 neighbours and we have to find a 64-node long path, so it would need to do (slightly less than) 8 ^ 64 steps to finish the whole algorithm.
Of course, if we would stop when we find the first solution it will be faster, but I still decided that there must be a better solution.
Greedy Algorithm
After thinking on it a while, I decided that it should be possible to find a solution using a greedy algorithm with an appropriate selection heuristic.
The first heuristic that I tried was to always try to go towards the bottom of the board and slowly fill in from there. After fighting a little with the GraphScript language, I wrote the following procedure:
CREATE OR REPLACE PROCEDURE "FIND_HAMILTONIAN_PATH" (
IN iv_origin VARCHAR(2),
OUT ot_path tt_path
) LANGUAGE GRAPH READS SQL DATA AS
BEGIN
Graph lo_graph = Graph("BOARD");
BigInt lv_size = Count(Vertices(:lo_graph));
-- retrieve the start point from the graph based on the origin label
Vertex lo_current = Vertex(:lo_graph, :iv_origin);
Sequence<Vertex> lt_nodes = [:lo_current];
ALTER lo_graph ADD TEMPORARY VERTEX ATTRIBUTE(Boolean visited = false);
WHILE (COUNT(:lt_nodes) <= :lv_size) {
lo_current."VISITED" = true;
Boolean lf_found = false;
Int lv_row = -1;
Int lv_col = -1;
FOREACH lo_neighbor IN NEIGHBORS(:lo_graph, { :lo_current }, 1, 1) {
-- first try to go on lower rows
-- if the row is the same, go towards the left corner
IF (NOT :lo_neighbor."VISITED"
AND (:lv_row < :lo_neighbor."ROW_NUMBER"
OR (:lv_row == :lo_neighbor."ROW_NUMBER"
AND :lv_col < :lo_neighbor."COL_NUMBER"))) {
lv_row = :lo_neighbor."ROW_NUMBER";
lv_col = :lo_neighbor."COL_NUMBER";
lf_found = true;
lo_current = :lo_neighbor;
}
}
-- stop the loop if we did not find a next node
-- this avoids infinite loops which do not do anything
IF (NOT :lf_found) {
BREAK;
}
-- append the next node to the path
lt_nodes = :lt_nodes || [:lo_current];
}
ot_path = SELECT :lo_node.label FOREACH lo_node IN :lt_nodes;
END;Unfortunately, this approach failed miserably, yielding mediocre results:

The problem looked to me like once the bottom half of the board was almost full, the knight got into a dead end. To prevent this, I tried applying a different heuristic: to always go as close as possible to the center of the board.
CREATE OR REPLACE PROCEDURE "FIND_HAMILTONIAN_PATH" (
IN iv_origin VARCHAR(2),
OUT ot_path tt_path
) LANGUAGE GRAPH READS SQL DATA AS
BEGIN
Graph lo_graph = Graph("BOARD");
-- get the size of the graph and use it throughout the algorithm
BigInt lv_size = Count(Vertices(:lo_graph));
-- retrieve the start point from the graph based on the origin label
Vertex lo_current = Vertex(:lo_graph, :iv_origin);
Sequence<Vertex> lt_nodes = [:lo_current];
ALTER lo_graph ADD TEMPORARY VERTEX ATTRIBUTE(Boolean visited = false);
WHILE (COUNT(:lt_nodes) <= :lv_size) {
lo_current."VISITED" = true;
Boolean lf_found = false;
BigInt lv_score = 4L * :lv_size;
FOREACH lo_neighbor IN NEIGHBORS(:lo_graph, { :lo_current }, 1, 1) {
IF (NOT :lo_neighbor."VISITED") {
-- compute the delta (4.5 would be the middle of the board, but we
-- multiply everything by 2 to be able to use integers)
BigInt lv_row_delta = 2L * BIGINT(:lo_neighbor."ROW_NUMBER") - 9L;
-- do an ABS, because GraphScript does not support math functions
IF (:lv_row_delta < 0L) {
lv_row_delta = :lv_row_delta * -1L;
}
BigInt lv_col_delta = 2L * BIGINT(:lo_neighbor."COL_NUMBER") - 9L;
IF (:lv_col_delta < 0L) {
lv_col_delta = :lv_col_delta * -1L;
}
IF (:lv_score > :lv_col_delta + :lv_row_delta) {
lv_score = :lv_col_delta + :lv_row_delta;
lo_current = :lo_neighbor;
lf_found = true;
}
}
}
IF (NOT :lf_found) {
BREAK;
}
-- append the next node to the path
lt_nodes = :lt_nodes || [:lo_current];
}
ot_path = SELECT :lo_node.label FOREACH lo_node IN :lt_nodes;
END;I envisioned that the knight will spin around the center of the board. What I did not realise is that this approach would basically cut off the corners of the board leading the knight to be stuck in one of the corners:

Seeing that my heuristics are not working, I decided to read a little literature on the topic.
Warnsdorff Rule
Source: Squirrel, Douglas, and Paul Çull. "A Warnsdorff-Rule Algorithm for Knight's Tours." (1996).
After reading some papers, I found out that I was very close to a correct solution. The heuristic that I was searching for was to always select the next node to be the one with the smallest degree. That is, we select the node which has the smallest amount of not-yet-visited neighbours.
CREATE OR REPLACE PROCEDURE "FIND_HAMILTONIAN_PATH_VIA_WARNSDORFF" (
IN iv_origin VARCHAR(2),
OUT ot_path tt_path
) LANGUAGE GRAPH READS SQL DATA AS
BEGIN
Graph lo_graph = Graph("BOARD");
-- get the size of the graph and use it throughout the algorithm
BigInt lv_size = Count(Vertices(:lo_graph));
-- retrieve the start point from the graph based on the origin label
Vertex lo_current = Vertex(:lo_graph, :iv_origin);
Sequence<Vertex> lt_nodes = [:lo_current];
ALTER lo_graph ADD TEMPORARY VERTEX ATTRIBUTE(Boolean visited = false);
WHILE (COUNT(:lt_nodes) <= :lv_size) {
lo_current.visited = true;
Boolean lf_found = false;
BigInt lv_min = :lv_size;
FOREACH lo_first IN NEIGHBORS(:lo_graph, { :lo_current }, 1, 1) {
IF (NOT :lo_first.visited) {
BigInt lv_first_count = 0L;
-- compute the degree of each neighbour
FOREACH lo_second IN NEIGHBORS(:lo_graph, { :lo_first }, 1, 1) {
IF (NOT :lo_second.visited AND :lo_second != :lo_current) {
lv_first_count = :lv_first_count + 1L;
}
}
-- go for the minimal degree
IF (:lv_first_count < :lv_min) {
lo_current = :lo_first;
lv_min = :lv_first_count;
lf_found = true;
}
}
}
IF (NOT :lf_found) {
BREAK;
}
-- append the next node to the path
lt_nodes = :lt_nodes || [:lo_current];
}
ot_path = SELECT :lo_node.label FOREACH lo_node IN :lt_nodes;
END;Basically, this would yield the exact opposite result as the image above: first visit the margins of the board, then the center:

I finally got a solution! But what I don't like at this heuristic is the fact that, when we have to decide on the next node and there are two nodes with the exact same score, we always take the first one. In the literature they usually take one at random, but there is no RANDOM function in GraphScript.
Sometimes this heuristic may not be able to yield a result (although I never encountered this situation), so I wanted to improve it further.
Pohl's Tie Breaking
Source: Pohl, Ira. "A method for finding Hamilton paths and Knight's tours." (1967).
One possible way of breaking ties would be to repeatedly apply the selection mechanism on the candidate nodes. Because I cannot really write a recursive call using GraphScript, I decided to go for a single level tie-breaking:
- First find all candidate nodes based on the Warnsdorff rule.
- If there is only one candidate, select that one.
- Otherwise, compute the minimal neighbour degree for each candidate and select the one with the smallest value. At this point, we could again reach a tie, so we just select the first one (this would be solved via recursion - except for the perfectly symmetrical arrangements).
CREATE OR REPLACE PROCEDURE "FIND_HAMILTONIAN_PATH_VIA_WARNSDORFF_AND_POHL" (
IN iv_origin VARCHAR(2),
OUT ot_path tt_path
) LANGUAGE GRAPH READS SQL DATA AS
BEGIN
Graph lo_graph = Graph("BOARD");
-- get the size of the graph and use it throughout the algorithm
BigInt lv_size = Count(Vertices(:lo_graph));
-- retrieve the start point from the graph based on the origin label
Vertex lo_current = Vertex(:lo_graph, :iv_origin);
Sequence<Vertex> lt_nodes = [:lo_current];
ALTER lo_graph ADD TEMPORARY VERTEX ATTRIBUTE(Boolean visited = false);
WHILE (COUNT(:lt_nodes) <= :lv_size) {
lo_current.visited = true;
BigInt lv_min = :lv_size;
-- we will use this sequence to store candidate nodes
Sequence<Vertex> lt_candidates = Sequence<Vertex>(:lo_graph);
FOREACH lo_first IN NEIGHBORS(:lo_graph, { :lo_current }, 1, 1) {
IF (NOT :lo_first.visited) {
BigInt lv_first_count = 0L;
-- compute the degree of each candidate
FOREACH lo_second IN NEIGHBORS(:lo_graph, { :lo_first }, 1, 1) {
IF (NOT :lo_second.visited) {
lv_first_count = :lv_first_count + 1L;
}
}
-- add the candidate to the list if needed
IF (:lv_first_count < :lv_min) {
lv_min = :lv_first_count;
lt_candidates = [ :lo_first ];
} ELSE {
IF (:lv_first_count == :lv_min) {
lt_candidates = :lt_candidates || [ :lo_first ];
}
}
}
}
-- terminate the algorithm if no candidates were found
IF (COUNT(:lt_candidates) == 0L) {
BREAK;
} ELSE {
-- select the single candidate if only one was found
IF (COUNT(:lt_candidates) == 1L) {
lo_current = :lt_candidates[1L];
-- otherwise, apply the tie-breaking heuristic
} ELSE {
lv_min = :lv_size;
FOREACH lo_candidate IN :lt_candidates {
BigInt lv_candidate_min = :lv_size;
-- find the minimum neighbour degree for each candidate
FOREACH lo_first IN NEIGHBORS(:lo_graph, {:lo_candidate}, 1, 1) {
BigInt lv_first_count = 0L;
IF (NOT :lo_first.visited) {
FOREACH lo_second IN NEIGHBORS(:lo_graph, {:lo_first}, 1, 1) {
IF (NOT :lo_second.visited AND :lo_second != :lo_candidate) {
lv_first_count = :lv_first_count + 1L;
}
}
}
IF (:lv_first_count < :lv_candidate_min) {
lv_candidate_min = :lv_first_count;
}
}
-- select the candidate with the smallest minimum neighbour degree
IF (:lv_candidate_min <= :lv_min) {
lo_current = :lo_candidate;
lv_min = :lv_candidate_min;
}
}
}
}
-- add the next node to the path
lt_nodes = :lt_nodes || [:lo_current];
}
ot_path = SELECT :lo_node.label FOREACH lo_node IN :lt_nodes;
END;Running it seems to generate the expected result:

I still don't like this solution, because even for asymmetrical arrangements, we still have to take a random choice (due to the lack of recursion).
Roth's Tie Breaking
Source: Ganzfried, Sam. "A Simple Algorithm for Knight’s Tours." (2004).
Another idea for the tie breaking is to select from the candidate nodes based on the distance from the center of the board (take the node with the maximal distance to the center):
CREATE OR REPLACE PROCEDURE "FIND_HAMILTONIAN_PATH_VIA_WARNSDORFF_AND_ROTH" (
IN iv_origin VARCHAR(2),
OUT ot_path tt_path
) LANGUAGE GRAPH READS SQL DATA AS
BEGIN
Graph lo_graph = Graph("BOARD");
-- get the size of the graph and use it throughout the algorithm
BigInt lv_size = Count(Vertices(:lo_graph));
-- retrieve the start point from the graph based on the origin label
Vertex lo_current = Vertex(:lo_graph, :iv_origin);
Sequence<Vertex> lt_nodes = [:lo_current];
ALTER lo_graph ADD TEMPORARY VERTEX ATTRIBUTE(Boolean visited = false);
WHILE (COUNT(:lt_nodes) <= :lv_size) {
lo_current.visited = true;
BigInt lv_min = :lv_size;
-- we will use this sequence to store candidate nodes
Sequence<Vertex> lt_candidates = Sequence<Vertex>(:lo_graph);
FOREACH lo_first IN NEIGHBORS(:lo_graph, { :lo_current }, 1, 1) {
IF (NOT :lo_first.visited) {
BigInt lv_first_count = 0L;
-- compute the degree of each candidate
FOREACH lo_second IN NEIGHBORS(:lo_graph, { :lo_first }, 1, 1) {
IF (NOT :lo_second.visited) {
lv_first_count = :lv_first_count + 1L;
}
}
-- add the candidate to the list if needed
IF (:lv_first_count < :lv_min) {
lv_min = :lv_first_count;
lt_candidates = [ :lo_first ];
} ELSE {
IF (:lv_first_count == :lv_min) {
lt_candidates = :lt_candidates || [ :lo_first ];
}
}
}
}
-- terminate the algorithm if no candidates were found
IF (COUNT(:lt_candidates) == 0L) {
BREAK;
} ELSE {
-- select the single candidate if only one was found
IF (COUNT(:lt_candidates) == 1L) {
lo_current = :lt_candidates[1L];
-- otherwise, apply the tie-breaking heuristic
} ELSE {
Double lv_max_distance = -1.0;
FOREACH lo_candidate IN :lt_candidates {
-- compute the distance between the vertex and the board center
Double lv_distance = (DOUBLE(:lo_candidate."ROW_NUMBER") - 4.5)
* (DOUBLE(:lo_candidate."ROW_NUMBER") - 4.5)
+ (DOUBLE(:lo_candidate."COL_NUMBER") - 4.5)
* (DOUBLE(:lo_candidate."COL_NUMBER") - 4.5);
-- select the candidate with maximal distance
IF (:lv_distance > :lv_max_distance ) {
lo_current = :lo_candidate;
lv_max_distance = :lv_distance;
}
}
}
}
-- add the next node to the path
lt_nodes = :lt_nodes || [:lo_current];
}
ot_path = SELECT :lo_node.label FOREACH lo_node IN :lt_nodes;
END;Surprisingly, running this for the same starting point generated the same result as Pohl's tie-breaking (most of the time).
Bloopers
I don't want to give a false impression and make people think that everything went smoothly. I actually encountered a few bugs and limitations which made me waste a few hours of my time:
- HANA Express is too large for my computer. I had to clean up 40GB of my laptop to be able to run it. I wanted to use HXE to have access to the latest service pack, but I really started thinking to use an older HANA to which I have access...
- I am not very happy with the fact that GraphScript is a completely different language than SQLScript, especially because of the fact that most functions available in SQLScript are not available in GraphScript. For example, there is no ABS in GraphScript.
- I did not find a way to pass a Graph object through the procedure interface (e.g. to create a recursive procedure).
- The WebIDE is always showing a ton of errors as if all the code is completely broken. To be honest, I would prefer to not have any kind of syntax check and just have syntax highlighting.
- Once I introduced the first IF clause, the WebIDE "Run" button would not anymore execute my "CREATE OR REPLACE PROCEDURE" statement. I had to resort to manually sending the code via an jQuery.ajax call from the development console.
jQuery.ajax({
method: "POST",
url: "/sap/hana/cst/api/v2/sessions(...)/connections(...)/sqlExecute()",
headers: {"X-CSRF-Token": "..."},
contentType: "application/json",
data: JSON.stringify({
"statements": [{"statement": code, "type": "UPDATE"}],
"maxResultSize": 1000,
"limitLOBColumnSize": 1024,
"includePosColumn": true,
"bExeWithoutPrepare": false,
"bStopOnError": true,
"bRunAsBackgroundActivity": false
})
});Conclusion
Overall, I think that working with the Graph Engine is fun, but it is still not a fully mature technology. Actually, this might apply to the whole XSA and not only to the Graph capabilities. Coming from the Java ecosystem, where you can have an excellent developer experience, developing on HANA using the WebIDE is somewhat lacklustre.
- SAP Managed Tags:
- SAP CodeJam,
- SAP TechEd,
- SAP HANA
8 Comments
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
Labels in this area
-
"automatische backups"
1 -
"regelmäßige sicherung"
1 -
"TypeScript" "Development" "FeedBack"
1 -
505 Technology Updates 53
1 -
ABAP
14 -
ABAP API
1 -
ABAP CDS Views
2 -
ABAP CDS Views - BW Extraction
1 -
ABAP CDS Views - CDC (Change Data Capture)
1 -
ABAP class
2 -
ABAP Cloud
2 -
ABAP Development
5 -
ABAP in Eclipse
1 -
ABAP Platform Trial
1 -
ABAP Programming
2 -
abap technical
1 -
absl
2 -
access data from SAP Datasphere directly from Snowflake
1 -
Access data from SAP datasphere to Qliksense
1 -
Accrual
1 -
action
1 -
adapter modules
1 -
Addon
1 -
Adobe Document Services
1 -
ADS
1 -
ADS Config
1 -
ADS with ABAP
1 -
ADS with Java
1 -
ADT
2 -
Advance Shipping and Receiving
1 -
Advanced Event Mesh
3 -
AEM
1 -
AI
7 -
AI Launchpad
1 -
AI Projects
1 -
AIML
9 -
Alert in Sap analytical cloud
1 -
Amazon S3
1 -
Analytical Dataset
1 -
Analytical Model
1 -
Analytics
1 -
Analyze Workload Data
1 -
annotations
1 -
API
1 -
API and Integration
3 -
API Call
2 -
Application Architecture
1 -
Application Development
5 -
Application Development for SAP HANA Cloud
3 -
Applications and Business Processes (AP)
1 -
Artificial Intelligence
1 -
Artificial Intelligence (AI)
5 -
Artificial Intelligence (AI) 1 Business Trends 363 Business Trends 8 Digital Transformation with Cloud ERP (DT) 1 Event Information 462 Event Information 15 Expert Insights 114 Expert Insights 76 Life at SAP 418 Life at SAP 1 Product Updates 4
1 -
Artificial Intelligence (AI) blockchain Data & Analytics
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise Oil Gas IoT Exploration Production
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise sustainability responsibility esg social compliance cybersecurity risk
1 -
ASE
1 -
ASR
2 -
ASUG
1 -
Attachments
1 -
Authorisations
1 -
Automating Processes
1 -
Automation
2 -
aws
2 -
Azure
1 -
Azure AI Studio
1 -
B2B Integration
1 -
Backorder Processing
1 -
Backup
1 -
Backup and Recovery
1 -
Backup schedule
1 -
BADI_MATERIAL_CHECK error message
1 -
Bank
1 -
BAS
1 -
basis
2 -
Basis Monitoring & Tcodes with Key notes
2 -
Batch Management
1 -
BDC
1 -
Best Practice
1 -
bitcoin
1 -
Blockchain
3 -
bodl
1 -
BOP in aATP
1 -
BOP Segments
1 -
BOP Strategies
1 -
BOP Variant
1 -
BPC
1 -
BPC LIVE
1 -
BTP
12 -
BTP Destination
2 -
Business AI
1 -
Business and IT Integration
1 -
Business application stu
1 -
Business Application Studio
1 -
Business Architecture
1 -
Business Communication Services
1 -
Business Continuity
1 -
Business Data Fabric
3 -
Business Partner
12 -
Business Partner Master Data
10 -
Business Technology Platform
2 -
Business Trends
4 -
CA
1 -
calculation view
1 -
CAP
3 -
Capgemini
1 -
CAPM
1 -
Catalyst for Efficiency: Revolutionizing SAP Integration Suite with Artificial Intelligence (AI) and
1 -
CCMS
2 -
CDQ
12 -
CDS
2 -
Cental Finance
1 -
Certificates
1 -
CFL
1 -
Change Management
1 -
chatbot
1 -
chatgpt
3 -
CL_SALV_TABLE
2 -
Class Runner
1 -
Classrunner
1 -
Cloud ALM Monitoring
1 -
Cloud ALM Operations
1 -
cloud connector
1 -
Cloud Extensibility
1 -
Cloud Foundry
4 -
Cloud Integration
6 -
Cloud Platform Integration
2 -
cloudalm
1 -
communication
1 -
Compensation Information Management
1 -
Compensation Management
1 -
Compliance
1 -
Compound Employee API
1 -
Configuration
1 -
Connectors
1 -
Consolidation Extension for SAP Analytics Cloud
2 -
Control Indicators.
1 -
Controller-Service-Repository pattern
1 -
Conversion
1 -
Cosine similarity
1 -
cryptocurrency
1 -
CSI
1 -
ctms
1 -
Custom chatbot
3 -
Custom Destination Service
1 -
custom fields
1 -
Customer Experience
1 -
Customer Journey
1 -
Customizing
1 -
cyber security
3 -
Data
1 -
Data & Analytics
1 -
Data Aging
1 -
Data Analytics
2 -
Data and Analytics (DA)
1 -
Data Archiving
1 -
Data Back-up
1 -
Data Governance
5 -
Data Integration
2 -
Data Quality
12 -
Data Quality Management
12 -
Data Synchronization
1 -
data transfer
1 -
Data Unleashed
1 -
Data Value
8 -
database tables
1 -
Datasphere
2 -
datenbanksicherung
1 -
dba cockpit
1 -
dbacockpit
1 -
Debugging
2 -
Delimiting Pay Components
1 -
Delta Integrations
1 -
Destination
3 -
Destination Service
1 -
Developer extensibility
1 -
Developing with SAP Integration Suite
1 -
Devops
1 -
digital transformation
1 -
Documentation
1 -
Dot Product
1 -
DQM
1 -
dump database
1 -
dump transaction
1 -
e-Invoice
1 -
E4H Conversion
1 -
Eclipse ADT ABAP Development Tools
2 -
edoc
1 -
edocument
1 -
ELA
1 -
Embedded Consolidation
1 -
Embedding
1 -
Embeddings
1 -
Employee Central
1 -
Employee Central Payroll
1 -
Employee Central Time Off
1 -
Employee Information
1 -
Employee Rehires
1 -
Enable Now
1 -
Enable now manager
1 -
endpoint
1 -
Enhancement Request
1 -
Enterprise Architecture
1 -
ETL Business Analytics with SAP Signavio
1 -
Euclidean distance
1 -
Event Dates
1 -
Event Driven Architecture
1 -
Event Mesh
2 -
Event Reason
1 -
EventBasedIntegration
1 -
EWM
1 -
EWM Outbound configuration
1 -
EWM-TM-Integration
1 -
Existing Event Changes
1 -
Expand
1 -
Expert
2 -
Expert Insights
2 -
Fiori
14 -
Fiori Elements
2 -
Fiori SAPUI5
12 -
Flask
1 -
Full Stack
8 -
Funds Management
1 -
General
1 -
General Splitter
1 -
Generative AI
1 -
Getting Started
1 -
GitHub
8 -
Grants Management
1 -
groovy
1 -
GTP
1 -
HANA
6 -
HANA Cloud
2 -
Hana Cloud Database Integration
2 -
HANA DB
2 -
HANA XS Advanced
1 -
Historical Events
1 -
home labs
1 -
HowTo
1 -
HR Data Management
1 -
html5
8 -
HTML5 Application
1 -
Identity cards validation
1 -
idm
1 -
Implementation
1 -
input parameter
1 -
instant payments
1 -
Integration
3 -
Integration Advisor
1 -
Integration Architecture
1 -
Integration Center
1 -
Integration Suite
1 -
intelligent enterprise
1 -
iot
1 -
Java
1 -
job
1 -
Job Information Changes
1 -
Job-Related Events
1 -
Job_Event_Information
1 -
joule
4 -
Journal Entries
1 -
Just Ask
1 -
Kerberos for ABAP
8 -
Kerberos for JAVA
8 -
KNN
1 -
Launch Wizard
1 -
learning content
2 -
Life at SAP
5 -
lightning
1 -
Linear Regression SAP HANA Cloud
1 -
local tax regulations
1 -
LP
1 -
Machine Learning
2 -
Marketing
1 -
Master Data
3 -
Master Data Management
14 -
Maxdb
2 -
MDG
1 -
MDGM
1 -
MDM
1 -
Message box.
1 -
Messages on RF Device
1 -
Microservices Architecture
1 -
Microsoft Universal Print
1 -
Middleware Solutions
1 -
Migration
5 -
ML Model Development
1 -
Modeling in SAP HANA Cloud
8 -
Monitoring
3 -
MTA
1 -
Multi-Record Scenarios
1 -
Multiple Event Triggers
1 -
Neo
1 -
New Event Creation
1 -
New Feature
1 -
Newcomer
1 -
NodeJS
2 -
ODATA
2 -
OData APIs
1 -
odatav2
1 -
ODATAV4
1 -
ODBC
1 -
ODBC Connection
1 -
Onpremise
1 -
open source
2 -
OpenAI API
1 -
Oracle
1 -
PaPM
1 -
PaPM Dynamic Data Copy through Writer function
1 -
PaPM Remote Call
1 -
PAS-C01
1 -
Pay Component Management
1 -
PGP
1 -
Pickle
1 -
PLANNING ARCHITECTURE
1 -
Popup in Sap analytical cloud
1 -
PostgrSQL
1 -
POSTMAN
1 -
Process Automation
2 -
Product Updates
4 -
PSM
1 -
Public Cloud
1 -
Python
4 -
Qlik
1 -
Qualtrics
1 -
RAP
3 -
RAP BO
2 -
Record Deletion
1 -
Recovery
1 -
recurring payments
1 -
redeply
1 -
Release
1 -
Remote Consumption Model
1 -
Replication Flows
1 -
research
1 -
Resilience
1 -
REST
1 -
REST API
1 -
Retagging Required
1 -
Risk
1 -
Rolling Kernel Switch
1 -
route
1 -
rules
1 -
S4 HANA
1 -
S4 HANA Cloud
1 -
S4 HANA On-Premise
1 -
S4HANA
3 -
S4HANA_OP_2023
2 -
SAC
10 -
SAC PLANNING
9 -
SAP
4 -
SAP ABAP
1 -
SAP Advanced Event Mesh
1 -
SAP AI Core
8 -
SAP AI Launchpad
8 -
SAP Analytic Cloud Compass
1 -
Sap Analytical Cloud
1 -
SAP Analytics Cloud
4 -
SAP Analytics Cloud for Consolidation
3 -
SAP Analytics Cloud Story
1 -
SAP analytics clouds
1 -
SAP BAS
1 -
SAP Basis
6 -
SAP BODS
1 -
SAP BODS certification.
1 -
SAP BTP
21 -
SAP BTP Build Work Zone
2 -
SAP BTP Cloud Foundry
6 -
SAP BTP Costing
1 -
SAP BTP CTMS
1 -
SAP BTP Innovation
1 -
SAP BTP Migration Tool
1 -
SAP BTP SDK IOS
1 -
SAP Build
11 -
SAP Build App
1 -
SAP Build apps
1 -
SAP Build CodeJam
1 -
SAP Build Process Automation
3 -
SAP Build work zone
10 -
SAP Business Objects Platform
1 -
SAP Business Technology
2 -
SAP Business Technology Platform (XP)
1 -
sap bw
1 -
SAP CAP
2 -
SAP CDC
1 -
SAP CDP
1 -
SAP CDS VIEW
1 -
SAP Certification
1 -
SAP Cloud ALM
4 -
SAP Cloud Application Programming Model
1 -
SAP Cloud Integration for Data Services
1 -
SAP cloud platform
8 -
SAP Companion
1 -
SAP CPI
3 -
SAP CPI (Cloud Platform Integration)
2 -
SAP CPI Discover tab
1 -
sap credential store
1 -
SAP Customer Data Cloud
1 -
SAP Customer Data Platform
1 -
SAP Data Intelligence
1 -
SAP Data Migration in Retail Industry
1 -
SAP Data Services
1 -
SAP DATABASE
1 -
SAP Dataspher to Non SAP BI tools
1 -
SAP Datasphere
10 -
SAP DRC
1 -
SAP EWM
1 -
SAP Fiori
2 -
SAP Fiori App Embedding
1 -
Sap Fiori Extension Project Using BAS
1 -
SAP GRC
1 -
SAP HANA
1 -
SAP HCM (Human Capital Management)
1 -
SAP HR Solutions
1 -
SAP IDM
1 -
SAP Integration Suite
9 -
SAP Integrations
4 -
SAP iRPA
2 -
SAP Learning Class
1 -
SAP Learning Hub
1 -
SAP Odata
2 -
SAP on Azure
1 -
SAP PartnerEdge
1 -
sap partners
1 -
SAP Password Reset
1 -
SAP PO Migration
1 -
SAP Prepackaged Content
1 -
SAP Process Automation
2 -
SAP Process Integration
2 -
SAP Process Orchestration
1 -
SAP S4HANA
2 -
SAP S4HANA Cloud
1 -
SAP S4HANA Cloud for Finance
1 -
SAP S4HANA Cloud private edition
1 -
SAP Sandbox
1 -
SAP STMS
1 -
SAP successfactors
3 -
SAP SuccessFactors HXM Core
1 -
SAP Time
1 -
SAP TM
2 -
SAP Trading Partner Management
1 -
SAP UI5
1 -
SAP Upgrade
1 -
SAP Utilities
1 -
SAP-GUI
8 -
SAP_COM_0276
1 -
SAPBTP
1 -
SAPCPI
1 -
SAPEWM
1 -
sapmentors
1 -
saponaws
2 -
SAPS4HANA
1 -
SAPUI5
4 -
schedule
1 -
Secure Login Client Setup
8 -
security
9 -
Selenium Testing
1 -
SEN
1 -
SEN Manager
1 -
service
1 -
SET_CELL_TYPE
1 -
SET_CELL_TYPE_COLUMN
1 -
SFTP scenario
2 -
Simplex
1 -
Single Sign On
8 -
Singlesource
1 -
SKLearn
1 -
soap
1 -
Software Development
1 -
SOLMAN
1 -
solman 7.2
2 -
Solution Manager
3 -
sp_dumpdb
1 -
sp_dumptrans
1 -
SQL
1 -
sql script
1 -
SSL
8 -
SSO
8 -
Substring function
1 -
SuccessFactors
1 -
SuccessFactors Platform
1 -
SuccessFactors Time Tracking
1 -
Sybase
1 -
system copy method
1 -
System owner
1 -
Table splitting
1 -
Tax Integration
1 -
Technical article
1 -
Technical articles
1 -
Technology Updates
14 -
Technology Updates
1 -
Technology_Updates
1 -
terraform
1 -
Threats
1 -
Time Collectors
1 -
Time Off
2 -
Time Sheet
1 -
Time Sheet SAP SuccessFactors Time Tracking
1 -
Tips and tricks
2 -
toggle button
1 -
Tools
1 -
Trainings & Certifications
1 -
Transport in SAP BODS
1 -
Transport Management
1 -
TypeScript
2 -
ui designer
1 -
unbind
1 -
Unified Customer Profile
1 -
UPB
1 -
Use of Parameters for Data Copy in PaPM
1 -
User Unlock
1 -
VA02
1 -
Validations
1 -
Vector Database
2 -
Vector Engine
1 -
Visual Studio Code
1 -
VSCode
1 -
Web SDK
1 -
work zone
1 -
workload
1 -
xsa
1 -
XSA Refresh
1
- « Previous
- Next »
Related Content
- Onboarding Users in SAP Quality Issue Resolution in Technology Blogs by SAP
- Improvising Time Management in SAP S/4HANA Cloud: A Co-Innovation Solution in Technology Blogs by SAP
- IoT - Ultimate Data Cyber Security - with Enterprise Blockchain and SAP BTP 🚀 in Technology Blogs by Members
- It’s Official - SAP BTP is Again a Leader in G2’s Reports in Technology Blogs by SAP
- IBM SSO LDAP Users Login Issue in 4.3 SP04 patch2 in Technology Q&A
Top kudoed authors
| User | Count |
|---|---|
| 10 | |
| 9 | |
| 5 | |
| 4 | |
| 4 | |
| 3 | |
| 3 | |
| 3 | |
| 3 | |
| 3 |