Technical Articles

Stefan Mayer

October 12, 2018 5 minute read

ABAP Float to IEEE-754 Single Precision Conversion

Floating Point Arithmetic

I personally had very few encounters with floating points in ABAP, usually only in regards to calculating back and forth some values. I never paid any attention to the format of a floating point within or without ABAP. However recently we had a business requirement to provide calculated floating points in a Floating Point encoding of “IEEE-754 single precision” for a third party legacy system.

It was the first time (shame) I learned how floating points are represented by a machine. Just like Character encoding or Integer “encoding” the floating point number needs to be put in a machine readable binary format of a certain length. There are various formats to represent floats, the most common and widely used standard is the IEEE-754 dating from the year 1986 with a revision in 2008.
This standard describes the byte representation of a floating point in several byte length. Most interesting to me was the so called single precision format which uses 32 bits in total, which are split in the segments of

1 sign bit
8 bits for the exponent
23 bits for the mantissa/fraction/significand

As a side note, the double precision uses 64 bits with 11 bits exponent and 52 bits mantissa which enables the machine to calculate more precise.

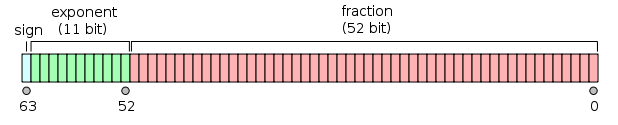
As an example we can take a decimal of 1742.5

IEEE-754 Single Precision:

0 10001001 10110011101000000000000

Hexadecimal 0x44d9d000

IEEE-754 Double Precision:

0 10000001001 1011001110100000000000000000000000000000000000000000

Hexadecimal 0x409B3A0000000000

Further read:

https://en.wikipedia.org/wiki/Floating-point_arithmetic

https://en.wikipedia.org/wiki/IEEE_754-1985

Floating Points in SAP ABAP

Disclaiming right away that I am no expert on ABAP data types, please let me know if the following statements are incorrect – I’d really like to be called out for a mistake.

My expectations regarding Floating Point data type in SAP ABAP have unfortunately been disappointed during research. I found the data type description in the help sites only mentioning the predefined data types

ABAP type	Standard	Implication
Decfloat16	IEEE-754-2008	Double Precision with 16 decimal places
Decfloat34	IEEE-754-2008	Quad Precision with 34 decimal places
f	IEEE-754 (not sure 1986/2008)	Double Precision

https://help.sap.com/doc/abapdocu_751_index_htm/7.51/en-US/abenbuiltin_types_numeric.htm

There is no hint given as to why single precision is not supported and I can only assume it is dismissed as double precision is sufficient for business requirements in SAP, however I wonder whether I am one of a few who deals with a legacy system and the requirement of storing floats in this specific byte representation.

Coming back to the example of decimal 1742.5. SAP ABAP represents a f type as

Exponent: 1.7425000000000000E+03

Hexadecimal 0x00000000003A9B40

Mind that the endian is different, if I shuffle the bytes it is: 0x409B3A0000… like above

Scaling down attempts

In a first attempt I naively tried to set the length to the data types defined; of course to no avail. I tried to find any conversion based on function modules etc. to scale down the precision to 32 bits. But of course it doesn’t make too much sense, one could probably do it; but how to handle large exponents? Rounding is a huge topic concerning infinite fractions (1/3, π etc.), too.

Again, note that if I make wrong assumptions, please let me know if I didn’t clearly grasp how to deal with the datatypes or if there are any conversions I didn’t find.

Converting human readable decimals to IEEE-754 single precision

I was only able to figure two alternatives at hand: Either do the math on a decimal number to shuffle the 32 bits into the correct encoding or to use a third party conversion library.

Both approaches have pros and cons. The Mathematical solution would be a custom solution which would be under our control and we’d be able to tackle any issues. However as this would be custom code (significant amount of lines) it would definitely take effort time wise to complete that task and it would take several iterations of testing and bug fixing and would require a good documentation and hand over. I also never quite tried to shuffle bits in ABAP so the learning curve needs to be taken.

The 3^rd party conversion library came to my mind as I did online researching on the topic and found diverse tools to do online float conversions between different formats, for example:

https://www.h-schmidt.net/FloatConverter/IEEE754.html

https://babbage.cs.qc.cuny.edu/IEEE-754.old/Decimal.html (including double precision)

http://www.binaryconvert.com/convert_float.html

The tools are mostly programmed in JavaScript or Python and for the figures I could compare I got the right results. My thought was to incorporate such a library to SAP and do the conversion. The benefits are: It is tested code, as a con I’d see that influencing the behavior would be a drag.

We need the conversion in the backend which limits our choices of programming languages. I personally do have some experience on JavaScript and considered code found on these sites and stackoverflow reasonably short and handy to convert floating points. I also discovered SAP offering a JavaScript engine to execute JavaScript server side within a ABAP class: CL_JAVA_SCRIPT.

https://blogs.sap.com/2006/10/16/abap-and-javascript/

All set and done?

Now with all aforementioned material I thought I have found a solid path to the goal of backend conversion. Alas here comes the nitty gritty of JavaScript, which I personally could overcome with some feats but maybe there is a different path I was not able to see.

The problems started off when I took my (few lines) of JavasScript code and had SAP interpret and run it. I didn’t want to fully understand the JavasScript engine, at first; I only wanted it to be a I/O machine of conversion. I got disappointed when the provided JavaScript code did not successfully execute. Problems obviously occurred with the syntax and data objects used in the snippet. The engine is most likely designed to take simple (old) JavaScript code. One would face the same problem with outdated browsers when executing JavaScript on a web site – so no blame on the engine.

Polyfilling the engine

As mentioned above the problem of running JavaScript in an outdated JavaScript run time is well known to web site owners as your provided JavaScript code is executed client-side and you cannot guarantee that all syntax and used objects/functions are available. To cope with missing APIs there is a technique called polyfill to replicate the functionality. There is a huge variety available for all kinds of problems and JavaScript versions

https://en.wikipedia.org/wiki/Polyfill_%28programming%29

I found a suitable polyfill at github called typedarray (https://github.com/inexorabletash/polyfill/blob/master/typedarray.js) which offers the missing Datatype of Float32. This finally enabled the conversion to execute successfully. Now I may pass a decimal value (currently as String) to be converted into a 32 bit IEEE-754 single precision hexadecimal.

Conclusion

The solution is there but it is undoubtedly not trivial and comes at a price. Mainly it is the maintenance and complexity I dislike. Yet, it enables us to unit-test the conversion to confirm the conversion result and a potential system update deviation. We may further use it in two independent systems without depending on client side conversion.

I cannot stress enough that I have doubts about the approach – that is why I intend to share this approach here to a critical audience. I didn’t find a quicker or more robust solution as of today. I would be very happy to get your thoughts and challenges on it. Maybe a built in process, code based on C? a web service?

If there is a ABAP kernel developer reading this piece – Might it be possible to have such a conversion or primitive data type available by any chance?

10 Comments

You must be Logged on to comment or reply to a post.

Matthew Billingham

October 12, 2018 at 12:52 pm

An interesting puzzle. Sorry, I don't have an answer-> perhaps Horst Keller can shed some light?

There are bit operations in ABAP, so it should be possible to write a routine that converts double precision into the correct form in an xstring.

Jelena Perfiljeva

October 12, 2018 at 8:26 pm

This might also be right up Karl Kessler 's alley. Not sure if he's checking SCN but I guess we're about to find out. 🙂

Marcin Makowski

October 12, 2018 at 1:02 pm

Thank you for inspiring me to do some research. I could not find solution with pure ABAP as well and I am excited to see what the others say. Good job with finding an alternative Stefan!

Sandra Rossi

October 12, 2018 at 4:21 pm

Your ABAP code could use a F data object, and convert it into a Single when it’s about generating the output. That should be quite easy, because it’s only about shrinking the exponent and the mantissa. A generic converter should take into account the byte order too. Here is the beginning of the code, that you may finish if you’re interested. Here, the Single is declared as a X type with 4 bytes, and the BE of single_be is for "big endian" (sign in first byte).

CLASS lcl_f DEFINITION.
  PUBLIC SECTION.
    TYPES ty_single TYPE x LENGTH 4.
    CLASS-METHODS convert_to_single_be
      IMPORTING
        f                       TYPE f
        tolerate_precision_loss TYPE abap_bool DEFAULT abap_true
      RETURNING
        VALUE(single_be)        TYPE ty_single
      EXCEPTIONS
        overflow
        precision_loss.
ENDCLASS.

CLASS lcl_f IMPLEMENTATION.

  METHOD convert_to_single_be.

    TYPES: ty_x4 TYPE x LENGTH 4,
           ty_x5 TYPE x LENGTH 5,
           ty_x8 TYPE x LENGTH 8.
    FIELD-SYMBOLS <f_x8> TYPE ty_x8.
    DATA: temp_x5 TYPE x LENGTH 5.

    CONSTANTS: low_29_bits                   TYPE x LENGTH 4 VALUE '1FFFFFFF',
               _00111000                     TYPE x LENGTH 1 VALUE '38',
               _01000000                     TYPE x LENGTH 1 VALUE '40',
               _11000000                     TYPE x LENGTH 1 VALUE 'C0',
               _11110000                     TYPE x LENGTH 1 VALUE 'F0',
               _0000011111111111             TYPE x LENGTH 2 VALUE '07FF',
               _00000111_4_bytes_eq_11111111 TYPE x LENGTH 5 VALUE '07FFFFFFFF'.

    "  abcdefgh ijklmnop qrstuvwx yzABCDEF
    "  ^        ^        ^        ^      ^
    " 31       23       15        7      0
    "
    " a is the sign ;
    " b is the sign of the exponent ;
    " cdefghi is the exponent ;
    " jklmnopqrstuvwxyzABCDEF is the mantissa ;
    "
    "  ab___cde fghijklm nopqrstu vwxyzABC DEF_____ ________ ________ ________
    "  ^        ^        ^        ^        ^        ^        ^        ^      ^
    " 63       55       47       39       31       23       15        7      0
    "
    " a is the sign ;
    " b is the sign of the exponent ;
    " ___cdefghi is the exponent ;
    " jklmnopqrstuvwxyzABCDEF________________________ is the mantissa ;


    DATA int8 TYPE int8.
    FIELD-SYMBOLS <f_x5> TYPE ty_x5.

    ASSIGN f TO <f_x8> CASTING.
    IF cl_abap_char_utilities=>endian = 'L'.
      DATA(x8) = CONV ty_x8( <f_x8>+7(1) && <f_x8>+6(1) && <f_x8>+5(1) && <f_x8>+4(1) && <f_x8>+3(1) && <f_x8>+2(1) && <f_x8>+1(1) && <f_x8>+0(1) ).
      ASSIGN x8 TO <f_x8> CASTING.
    ENDIF.

    IF <f_x8> O _01000000 AND NOT <f_x8> Z _00111000.
      RAISE overflow.
    ELSEIF <f_x8> Z _01000000 AND NOT <f_x8> O _00111000.
      RAISE overflow.
    ENDIF.

    IF tolerate_precision_loss = abap_false AND NOT <f_x8>+5 Z low_29_bits.
      RAISE precision_loss.
    ENDIF.

    " ab   (bits 31 to 30 <- bits 63 to 62)
    single_be(1) = <f_x8>(1) BIT-AND _11000000.

    " cdefghijklmnopqrstuvwxyzABCDEF
    temp_x5 = <f_x8>(5) BIT-AND _00000111_4_bytes_eq_11111111.
    temp_x5 = temp_x5 * CONV int8( 8 ). " shift left by 3 bits
    single_be = single_be BIT-OR temp_x5(4).

  ENDMETHOD.

ENDCLASS.

CLASS ltc_main DEFINITION
      FOR TESTING
      DURATION SHORT
      RISK LEVEL HARMLESS
      INHERITING FROM cl_aunit_assert.
  PRIVATE SECTION.

    METHODS test FOR TESTING.
    METHODS test2 FOR TESTING.
    METHODS overflow FOR TESTING.

    METHODS main
      IMPORTING
        f                       TYPE f
        tolerate_precision_loss TYPE abap_bool DEFAULT abap_true
        exp_single_be           TYPE lcl_f=>ty_single
        exp_overflow            TYPE abap_bool DEFAULT abap_false
        exp_precision_loss      TYPE abap_bool DEFAULT abap_false.

ENDCLASS.

CLASS ltc_main IMPLEMENTATION.

  METHOD test.
    main( f = '0.125' exp_single_be = '3E000000' ).
  ENDMETHOD.

  METHOD test2.
    main( f = '0.15625' exp_single_be = '3E200000' ).
  ENDMETHOD.

  METHOD overflow.
    main( f = '1E50' exp_single_be = '00' exp_overflow = abap_true ).
  ENDMETHOD.

  METHOD main.

    lcl_f=>convert_to_single_be(
      EXPORTING
        f                       = f
        tolerate_precision_loss = tolerate_precision_loss
      RECEIVING
        single_be               = DATA(single_be)
      EXCEPTIONS
        overflow                = 1
        precision_loss          = 2 ).
    CASE sy-subrc.
      WHEN 1. DATA(overflow) = abap_true.
      WHEN 2. DATA(precision_loss) = abap_true.
    ENDCASE.

    cl_abap_unit_assert=>assert_equals( act = single_be exp = exp_single_be ).
    cl_abap_unit_assert=>assert_equals( act = overflow exp = exp_overflow ).
    cl_abap_unit_assert=>assert_equals( act = precision_loss exp = exp_precision_loss ).

  ENDMETHOD.

ENDCLASS.

Stefan Mayer

Blog Post Author

October 31, 2018 at 9:40 am

Kudos to you Sandra for providing this method. You really saved my .. err day 😉

I admit I had to dig up some help sites to actually understand what happens syntax wise. I really appreciate your comments. I redid parts because of release limitation. I also had to revisit the bitmasks which I didn't see since university 😉

The approach to shrink or scale down the exponent and mantissa was in my mind all along but I never considered it seriously because I mistook the approach as dangerously. You really opened my eyes by introducing the check and the exceptions; that made it clear to me that there is of course a potential overflow if exponent uses the higher 3 bits (bits 3-5) and a potential precision issue in cases the mantiassa is used beyond bit 32. By checking and flagging the overflow and precision issue (or tolerating it) you are able to scale down the float and tell the caller.

In our business scenario I can imagine these cases to occur, especially the precision trouble in case the user sets a non terminating fraction (e.g. 1/3).

The code still is magic to me as it is much simpler than redoing the mathematical calculation based on the spec - Again Thank you so much and I am in debt to you. If you don't mind I will edit my post with a modified excerpt and some more comments for other readers. Let me know if you are not ok

best,

Stefan

Sandra Rossi

November 6, 2018 at 10:37 am

I just saw your comment. You're welcome, and I don't mind of course.

Jelena Perfiljeva

October 12, 2018 at 8:35 pm

This is very well done. Others have already commented on the technical side of it. I've actually never had to deal with floating decimal format not only in ABAP but anywhere else in life since I graduated many years ago. But as someone who inherited a mature SAP system at a company that actually invented their own encoding format (which I haven't even heard of before), I can feel your pain.

Really appreciated the whole story, from the background (why was this needed) through all the valleys of despair and mountains of hope. I probably would've taken the custom code route, so reading about your path is even more valuable.

There are not many people who can write like this. You should consider doing this more frequently. It's a gift. And Paul Hardy needs some competition. 🙂

Stefan Mayer

Blog Post Author

October 31, 2018 at 9:45 am

Kind of you to say so, I'm flattered. Maybe next time I write a post with a happy ending 🙂

Mark Teichmann

October 13, 2018 at 7:00 am

One quick remark regarding class CL_ABAP_JAVASCRIPT: It is advised to not use it in the future https://help.sap.com/doc/abapdocu_751_index_htm/7.51/en-US/abenabap_java_script.htm

Stefan Mayer

Blog Post Author

October 31, 2018 at 9:42 am

Yep thanks, good hint - I am sorry SAP doesn't consider it as a nice option to have a JS engine available. For as long as it is flagged as deprecated it is a bad practice to use it

Technical Articles

ABAP Float to IEEE-754 Single Precision Conversion

Floating Point Arithmetic

IEEE-754 Single Precision:

IEEE-754 Double Precision:

Floating Points in SAP ABAP

Scaling down attempts

Converting human readable decimals to IEEE-754 single precision

All set and done?

Polyfilling the engine

Conclusion

Assigned Tags