
- SAP Community
- Products and Technology
- Product Lifecycle Management
- PLM Blogs by Members
- Localization in SAP-MII Using UI5
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
A technology is truly beneficial only when it can be accessed by anyone and everyone without any language constraints.
The process of preparing an application to support more than one language and data format is called internationalization.
Localization is the process of adapting an internationalized application to support a specific region or locale. Examples of locale-dependent information include messages and user interface labels. Although all client user interfaces should be internationalized and localized, these processes are particularly important for web applications because of the global nature of the web.
In SAP MII as well, it is important to understand and put forth a process to deal with localization. Though localization is not new in MII. But apart from traditional localization approach of implementing in .irpt file, this blog talks about how localization can implemented for SAP MII UI developed in SAP UI 5”
Some of the questions that this blog will help to answer:
1.) How to create a .properties file?
2.) Where do we give the .properties file?
3.) What does oModel.getResourceBundle () do?
Before starting let’s get into the basics of localization (for those who are new) & some terms you will come across:
Internationalization: Designing and developing a software product to function in multiple locales. This process involves identifying the locales that must be supported, designing features which support those locales, and writing code that functions equally well in any of the supported locales.
Localization: Modifying or adapting a software product to fit the requirements of a particular locale. This process includes (but may not be limited to) translating the user interface.
i18n: Acronym for ‘internationalization’ (‘i’ + 18 letters + ‘n'; lower case i is used to distinguish it from the numeral 1 (one)).
Resource: Any part of a program which can appear to the user or be changed or configured by the user.
Core product: The language independent portion of a software product. Sometimes, however, this term is used to refer to the English product.
Let me come to the steps with a little description to make you understand how localization can be implemented in UI 5”
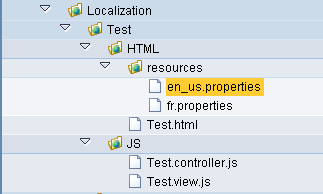
Step 1: Creating a Resource File
To completely localize our application, we'll need to gather a collection of strings appropriate for a locale and use them in appropriate places throughout the application. In order to assist us, the Java class library provides resource bundles.
.properties is a file extension for storing strings for localization, these are known as Property Resource Bundles.
Resource bundlesare a collection of*.propertiesfiles. All files are named with the same base name (prefix identifying the resource bundle), an optional suffix that identifies the language contained in each file and the fixed.propertiesextension.
A resource bundle file is a Java properties file. It contains key/value pairs where the values are the language-dependent texts and the keys are language independent text used by the application to identify and access the corresponding values.
When a localized text is needed, the application uses the SAPUI5 APIs to load the properties file that matches the current language best. To retrieve a text from the properties file, the application uses the (language-independent) key. If no text can be found for this key, the next best matching file is loaded and checked for the text. If no file matches, the raw file is loaded and checked.
Developer creates a .property file for the application; say, en_US. Please note that when we mention the property file as just "en", it is a culture without a region. And when we mention en_US, then it is "English with American English ", culture with region.
The resource bundle can consists of the following individual files:
- en.properties: Contains English text (without a specific country)
- en_US.properties: Contains text in American English
- en_UK.properties: Contains text in British English
For an example:
a. en_us.properties file

b. fr.properties file is created to support language type "French"

Step 2: Initialize Localization in View.js file
You can use the JavaScript module jQuery.sap.resources to access localized texts. The module contains APIs to load a resource bundle file from a given URL and for a given locale.
To make sure that the jQuery.sap.resources module is loaded you have to mention below in your code:

You can then use the jQuery.sap.resourcesfunction to load the resource bundle from the given URL, that is, the bundle name, and for a given locale. When no locale is specified, a default locale (en) is used. The following code snippet shows the use of thejQuery.sap.resourcesfunction to return a jQuery.sap.util.ResourceBundle:

Data Binding
You can also use data binding to access localized texts. The ResourceModel is a wrapper for resource bundles that exposes the localized texts as a model for data binding. You can use ResourceModel to bind text for properties to language dependent resource bundle properties. You can instantiate the ResourceModel either with bundleName (name of a resource bundle) or a bundleUrl, which points to a resource bundle. When you use the bundle name, make sure that the file has a .properties suffix. If no locale is defined, the current language is used. In this below example we are using bundleUrl:

/** Set the resource model with the symbolic name "i18n"

The coding of the test page looks as follows:
HTML Page:
Setting up the SAPUI5 bootstrap and required libraries in index.html file
Add the required libraries in the "data-sap-ui-libs" tag

- Test.View.js Page:

Language Type: ENGLISH

Language Type: French

- SAP Managed Tags:
- SAP Manufacturing Integration and Intelligence
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
- Local(DM) PRT material stock not getting updated on TOOL usage. in Product Lifecycle Management Q&A
- DMC POD Plugin local development environment in VS Code in Product Lifecycle Management Blogs by SAP
- How to use local routing operations to report a result to ERP? in Product Lifecycle Management Q&A
- Material report with US size and local size in Product Lifecycle Management Q&A
- How to refresh i5Grid after Model data has been updated locally in the page? in Product Lifecycle Management Q&A