
- SAP Community
- Products and Technology
- Technology
- Technology Blogs by Members
- Thinking in HANA - Part 1: Set Operators
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Hi Folks,
I've been mulling over a series of documents for a while now and finally have the bandwidth to put some of them together.
I've decided to group several of them under the idea of "Thinking in HANA". As a massively-parallel, column-oriented, in-memory platform, HANA affords many opportunities to come up with new and creative solutions to seemingly well-understood problems. Moreover, while HANA fully supports SQL-92, a majority of analytical use cases require efficient and often complex data models that support demanding BI requirements, which lead to several challenges:
- Complex data flows captured in hand-coded SQL and/or SQLScript can be difficult to maintain.
- SQL queries against raw tables, whether hand-coded or software-generated (i.e. from a semantic layer like BOBJ Universes), often fail to leverage native high-performance engines in HANA (i.e. OLAP/Calc Engine).
- While the "structure" of data models corresponds closely to well-understood relational operations (different join types, filters, aggregations, calculations), there are multiple cases where HANA does not behave in a strictly relational fashion, leading to potentially confusing results.
- Some SQL operators can't be modeled in HANA a 1:1 fashion. For example, UNION, EXCEPT/MINUS, and INTERSECT set operators are unavailable as node types in HANA Calculation Views.
This first article will review point 4 above - how to model database set operators (UNION, EXCEPT, INTERSECT) though a straightforward Calculation View "pattern". I also intend on fleshing out some of the theoretical implications of "set operator" thinking in HANA. Also, while set operators such as MINUS and INTERSECT aren't commonly required for meeting analytical needs on HANA, they do have implications for other more frequent requirements. I'll elaborate on these in another article.
The assumption is that the readers have a basic understanding of SQL, Set Theory, and data modeling in HANA.
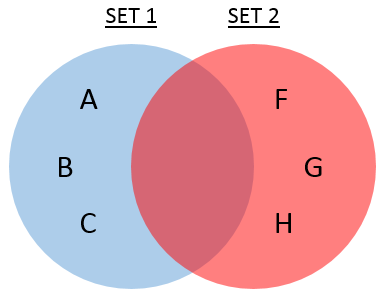
Sets – Brief Review
The following Venn Diagram gives a very simple example of how two sets might relate, having some elements in common but some unique to each set.

In the business world there are many cases where two data sets want to be compared - i.e. planned and actual sales figures, sales amounts and invoiced amounts, and many others.
In terms of comparing two sets of data, the following questions can be asked (and answered):
1) What are all the elements in both data sets?
2) Which elements are exclusive to SET 1?
3) Which elements are exclusive to SET 2?
4) Which elements are in both sets?
5) Which elements are in SET 1 (non-exclusive)?
6) Which elements are in SET 2 (non-exclusive)?
7) Which elements are in SET 1 or SET 2?
The questions above are answered below, with solutions in: 1) plain SQL, 2) 'alternate' SQL, and 3) Calculation View approach. The solutions are illustrated with their respective Venn diagrams and associated set operators.
'Alternate' SQL is SQL that reaches the same answer but uses the same logic flow as the Calculation View. It facilitates the "jump" from traditional SQL to HANA data modeling.
Please see the appendix of this document for the SQL to generate both data sets.
Basic Set Operators
The first four questions posed above are answered (solved) below. The solutions leverage the basic set operations of UNION, MINUS, and INTERSECT. (Here no distinction is made between UNION and UNION ALL). The last three of the seven questions above are solved in a “compound” fashion, built with more than one of the basic set operators.
1. What are the elements in both data sets?

SQL Solution
-- UNION (ALL)
SELECT *
FROM
(
SELECT ELEMENT
FROM SET_1
UNION ALL
SELECT ELEMENT
FROM SET_2
)
ORDER BY ELEMENT;
Alternate SQL Solution
None
Calculation View Solution
The Calculation View simply requires combining both data sets via UNION node. Despite the name, the UNION behaves as UNION ALL.
2. Which elements are exclusive to SET 1?

SQL Solution
-- Complement of Set 2 with respect to Set 1
SELECT *
FROM
(
SELECT ELEMENT
FROM SET_1
MINUS -- EXCEPT also works
SELECT ELEMENT
FROM SET_2
)
ORDER BY ELEMENT;
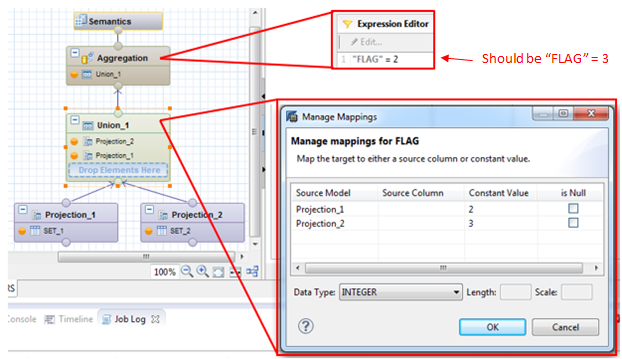
Alternate SQL Solution
-- Complement of Set 2 with respect to Set 1
-- UNION (ALL)
SELECT ELEMENT
FROM
(
SELECT ELEMENT, 2 AS FLAG
FROM SET_1
UNION ALL
SELECT ELEMENT, 3 AS FLAG
FROM SET_2
)
GROUP BY ELEMENT
HAVING SUM(FLAG) = 2
ORDER BY ELEMENT;
Calculation View Solution
The Calculation View accomplishes the same logic as the Alternate SQL – adding constant values to each data set, aggregating, and then filtering for result records where aggregate value of FLAG column is equal to the constant for the desired data set.

3. Which elements are exclusive to SET 2?
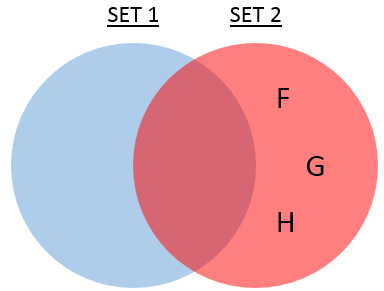
SQL Solution
-- Complement of Set 1 with respect to Set 2
SELECT *
FROM
(
SELECT ELEMENT
FROM SET_2
EXCEPT
SELECT ELEMENT
FROM SET_1
)
ORDER BY ELEMENT;
Alternate SQL Solution
-- Complement of Set 1 with respect to Set 2
SELECT ELEMENT
FROM
(
SELECT ELEMENT, 2 AS FLAG
FROM SET_1
UNION ALL
SELECT ELEMENT, 3 AS FLAG
FROM SET_2
)
GROUP BY ELEMENT
HAVING SUM(FLAG) = 3
ORDER BY ELEMENT;
Calculation View Solution
Note that the solution approach is the same as previously except with a filter for SET 2’s constant value rather than that of SET 1
4. Which elements are in both sets?

SQL Solution
-- intersection of Set 1 and Set 2
SELECT *
FROM
(
SELECT ELEMENT
FROM SET_1
INTERSECT
SELECT ELEMENT
FROM SET_2
)
ORDER BY ELEMENT;
Alternate SQL Solution
-- Intersection of Sets 1 and 2
SELECT ELEMENT
FROM
(
SELECT ELEMENT, 2 AS FLAG
FROM SET_1
UNION ALL
SELECT ELEMENT, 3 AS FLAG
FROM SET_2
)
GROUP BY ELEMENT
HAVING SUM(FLAG) = 5
ORDER BY ELEMENT;
Calculation View Solution

Note that the solution approach is the same as previously except with a filter for FLAG = 5 to capture only those records that fall under both (i.e. 2+3 = 5, hence capturing only overlapping (intersecting) records).
Compound Set Operations
Solutions for question 5-7 are solved by applying more than one basic set operator. As such, these solutions are referred to as “compound set operations”.
5. Which elements are in SET 1 (non-exclusive)?

SQL Solution
SELECT *
FROM
(
(
SELECT ELEMENT
FROM SET_1
EXCEPT
SELECT ELEMENT
FROM SET_2
)
UNION ALL
(
SELECT ELEMENT
FROM SET_1
INTERSECT
SELECT ELEMENT
FROM SET_2
)
)
ORDER BY ELEMENT;
Alternate SQL Solution
SELECT ELEMENT
FROM
(
SELECT ELEMENT, 2 AS FLAG
FROM SET_1
UNION ALL
SELECT ELEMENT, 3 AS FLAG
FROM SET_2
)
GROUP BY ELEMENT
HAVING SUM(FLAG) IN (2, 5)
ORDER BY ELEMENT;
Calculation View Solution

6. Which elements are in SET 2 (non-exclusive)?

SQL Solution
SELECT *
FROM
(
(
SELECT ELEMENT
FROM SET_2
EXCEPT
SELECT ELEMENT
FROM SET_1
)
UNION ALL
(
SELECT ELEMENT
FROM SET_1
INTERSECT
SELECT ELEMENT
FROM SET_2
)
)
ORDER BY ELEMENT;
Alternate SQL Solution
SELECT ELEMENT
FROM
(
SELECT ELEMENT, 2 AS FLAG
FROM SET_1
UNION ALL
SELECT ELEMENT, 3 AS FLAG
FROM SET_2
)
GROUP BY ELEMENT
HAVING SUM(FLAG) IN (3, 5)
ORDER BY ELEMENT;
Calculation View Solution

7. Which elements are in SET 1 or SET 2?
SQL Solution
SELECT *
FROM
(
(
SELECT ELEMENT
FROM SET_1
EXCEPT
SELECT ELEMENT
FROM SET_2
)
UNION ALL
(
SELECT ELEMENT
FROM SET_2
EXCEPT
SELECT ELEMENT
FROM SET_1
)
)
ORDER BY ELEMENT;
Alternate SQL Solution
SELECT ELEMENT
FROM
(
SELECT ELEMENT, 2 AS FLAG
FROM SET_1
UNION ALL
SELECT ELEMENT, 3 AS FLAG
FROM SET_2
)
GROUP BY ELEMENT
HAVING SUM(FLAG) != 5
ORDER BY ELEMENT;
Calculation View Solution

Discussion
A few points are worthy of additional discussion:
Over-engineered solution?
The astute reader will note that the solutions for problems (questions) 6 and 7 could easily be achieved by simply querying SET_1 or SET_2 by themselves. This is true. However, from a theoretical perspective, capturing duplicates would still require inspecting SET_1 and SET_2. According to the HANA SQL guide, EXCEPT/MINUS/INTERSECT can operate “as such”, or with DISTINCT keyword. Unfortunately, they still function as distinct without the DISTINCT keyword – making it so that solutions 6 or 7 can’t be properly achieved if duplicates are required for any reasons. This is a bit pedantic though – as duplicates almost never need to be reported (and they could still be captured through more complex SQL).
Empty set
The number of possible “locations” of an element is 3 – i.e. in SET_1, SET_2, or both. An element can either exist, or not exist, in those three locations. This means that 8 outcomes are possible, calculated as 2^3, where 2 is the number of states (exists or not exists) and 3 is the number of “locations”. In the above examples, only 7 questions are addressed as the “empty set” is not a relevant question in the context of analytics for this discussion.
The eight possibilities can also be captured in the following table. Empty set is grayed out:
In SET 1 | In SET 2 | In both sets | |
1 | FALSE | FALSE | FALSE |
2 | FALSE | FALSE | TRUE |
3 | FALSE | TRUE | FALSE |
4 | FALSE | TRUE | TRUE |
5 | TRUE | FALSE | FALSE |
6 | TRUE | FALSE | TRUE |
7 | TRUE | TRUE | FALSE |
8 | TRUE | TRUE | TRUE |
Identifying Possibilities (Advanced)
The following discussion is for the sake of theoretical curiosity rather than an actual pragmatic solution. The problem is partially solved, left to readers smarter than myself to answer.
Consider the following Venn diagram, particularly the sections in green.

How would you go about finding the elements associated with the green sections above? Visually we can see that it’s A, G and D – but what if each set had many elements and we had to solve this situation with SQL?
First note that set operators like UNION and INTERSECTION correlate with the Boolean operations OR and AND. Moreover, databases have helpful operations like IN and BETWEEN which essentially reduce to combinations of ANDs and ORs. In solutions highlighted above in this paper, some “Boolean logic” was implemented in set operators (UNION, MINUS, etc), and some in the filter condition to meet the final output. The question is – can all of the logic be implemented in set operations, with a filter on a single value that identifies all possible combinations? In our diagram above – rather than building confusing SQL (or Calc Views) with various set operations, and filtering further with Boolean logic – could we simply identify a single value assigned to that combination, and filter on that value? The answer is yes. It’s not pragmatic, but is interesting to note that it’s possible.
Here’s a simplified version that shows the direction of the solution – although not yet fully implemented. Note that this simplest-case becomes very complex – highlighting unpractical it is – but also illustrating the “elegance” assigned to mathematics that’s often easy to miss.
Consider the following Venn diagram:

As noted previously, there are eight possible situations for any single element. In previous solutions we assigned “constant values” to each base set, combined them, and then filtered in order to arrive at a desired result. You may have noticed that the numbers used, 2 and 3, are prime numbers – which indicates the direction of a more robust solution.
Simply aggregating numbers, even when prime, does not guarantee a unique outcome. If three sets are available, a developer were to use the first three prime numbers: 2, 3, and 5 – it’s clear that aggregating 2 and 3 would equal 5 – causing problematic results (potentially) if a similar approach were used as previously in this paper.
The solution approach (unfinished) then is as follows:
- 1) Assign a prime number constant value to each source set. Set the constant value of other source sets equal to 1.
- 2) Aggregate the sets, and add a calculated field equal to the product of the source set constant values. Since the source values are prime numbers greater to one (or one), this product is guaranteed unique.
- 3) Map this result to itself with a CROSS JOIN.
- 4) Multiply the calculated field by itself.
- 5) Query two fields from this set: ELEMENT (from either table in CROSS JOIN) and M_FLAG (where M_FLAG is the name I gave to the calculated field). Note that there is a distinct value assigned to each combination of records that fulfill 6 of the 8 possibilities (i.e. where values are found in one or two regions. The empty set, and the case of all three regions is not solved. Three CROSS JOINs, correlating to the three regions – solve the problem fully, but also result in redundant records).
- [ My intuition and some playing around with numbers indicates the following: The number of “regions” is a function of the number of sets N, defined by N * (N-1) + 1. Note: Thanks to josef.bodenschatz for noting that the function should actual be N^2 - 1. This holds for up to 4 sets (4 circles) and likely more. The number of “states” of an element it seems is the square of the number of “regions” based on the examples in this document. So in the case of four sets (four circles), that would make (4*4 - 1) ^ 2 = 225 combinations. Multiplying the first 169 prime numbers would result in a massive number, again indicating how unpractical this approach is. J
Run the following SQL, and note how a filter on ID = 6 would give you the “complement” of the sets, as one example.
DROP TABLE SETS_WITH_FLAGS;
CREATE COLUMN TABLE SETS_WITH_FLAGS AS
(
SELECT ELEMENT, MAX(FLAG_1) AS FLAG_1, MAX(FLAG_2) AS FLAG_2, (MAX(FLAG_1)*MAX(FLAG_2)) AS M_FLAG
FROM
(
SELECT 'A' AS ELEMENT, 2 AS FLAG_1, 1 AS FLAG_2 FROM DUMMY UNION ALL
SELECT 'B' AS ELEMENT, 2 AS FLAG_1, 1 AS FLAG_2 FROM DUMMY UNION ALL
SELECT 'B' AS ELEMENT, 1 AS FLAG_1, 3 AS FLAG_2 FROM DUMMY UNION ALL
SELECT 'C' AS ELEMENT, 1 AS FLAG_1, 3 AS FLAG_2 FROM DUMMY
)
GROUP BY ELEMENT
);
SELECT T2.ELEMENT, T1.M_FLAG * T2.M_FLAG AS ID FROM SET_FLAG T1 CROSS JOIN SET_FLAG T2 ORDER BY T1.M_FLAG * T2.M_FLAG;
Appendix
Following is the source data SQL used for the examples in this document.
DROP TABLE SET_1;
CREATE COLUMN TABLE SET_1
(
ELEMENT CHAR(1),
PRIMARY KEY (ELEMENT)
);
DROP TABLE SET_2;
CREATE COLUMN TABLE SET_2
(
ELEMENT CHAR(1),
PRIMARY KEY (ELEMENT)
);
INSERT INTO SET_1 VALUES ('A');
INSERT INTO SET_1 VALUES ('B');
INSERT INTO SET_1 VALUES ('C');
INSERT INTO SET_1 VALUES ('D');
INSERT INTO SET_1 VALUES ('E');
INSERT INTO SET_2 VALUES ('D');
INSERT INTO SET_2 VALUES ('E');
INSERT INTO SET_2 VALUES ('F');
INSERT INTO SET_2 VALUES ('G');
INSERT INTO SET_2 VALUES ('H');
- SAP Managed Tags:
- SAP HANA
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
-
"automatische backups"
1 -
"regelmäßige sicherung"
1 -
"TypeScript" "Development" "FeedBack"
1 -
505 Technology Updates 53
1 -
ABAP
14 -
ABAP API
1 -
ABAP CDS Views
2 -
ABAP CDS Views - BW Extraction
1 -
ABAP CDS Views - CDC (Change Data Capture)
1 -
ABAP class
2 -
ABAP Cloud
2 -
ABAP Development
5 -
ABAP in Eclipse
1 -
ABAP Platform Trial
1 -
ABAP Programming
2 -
abap technical
1 -
absl
1 -
access data from SAP Datasphere directly from Snowflake
1 -
Access data from SAP datasphere to Qliksense
1 -
Accrual
1 -
action
1 -
adapter modules
1 -
Addon
1 -
Adobe Document Services
1 -
ADS
1 -
ADS Config
1 -
ADS with ABAP
1 -
ADS with Java
1 -
ADT
2 -
Advance Shipping and Receiving
1 -
Advanced Event Mesh
3 -
AEM
1 -
AI
7 -
AI Launchpad
1 -
AI Projects
1 -
AIML
9 -
Alert in Sap analytical cloud
1 -
Amazon S3
1 -
Analytical Dataset
1 -
Analytical Model
1 -
Analytics
1 -
Analyze Workload Data
1 -
annotations
1 -
API
1 -
API and Integration
3 -
API Call
2 -
Application Architecture
1 -
Application Development
5 -
Application Development for SAP HANA Cloud
3 -
Applications and Business Processes (AP)
1 -
Artificial Intelligence
1 -
Artificial Intelligence (AI)
4 -
Artificial Intelligence (AI) 1 Business Trends 363 Business Trends 8 Digital Transformation with Cloud ERP (DT) 1 Event Information 462 Event Information 15 Expert Insights 114 Expert Insights 76 Life at SAP 418 Life at SAP 1 Product Updates 4
1 -
Artificial Intelligence (AI) blockchain Data & Analytics
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise Oil Gas IoT Exploration Production
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise sustainability responsibility esg social compliance cybersecurity risk
1 -
ASE
1 -
ASR
2 -
ASUG
1 -
Attachments
1 -
Authorisations
1 -
Automating Processes
1 -
Automation
1 -
aws
2 -
Azure
1 -
Azure AI Studio
1 -
B2B Integration
1 -
Backorder Processing
1 -
Backup
1 -
Backup and Recovery
1 -
Backup schedule
1 -
BADI_MATERIAL_CHECK error message
1 -
Bank
1 -
BAS
1 -
basis
2 -
Basis Monitoring & Tcodes with Key notes
2 -
Batch Management
1 -
BDC
1 -
Best Practice
1 -
bitcoin
1 -
Blockchain
3 -
BOP in aATP
1 -
BOP Segments
1 -
BOP Strategies
1 -
BOP Variant
1 -
BPC
1 -
BPC LIVE
1 -
BTP
11 -
BTP Destination
2 -
Business AI
1 -
Business and IT Integration
1 -
Business application stu
1 -
Business Application Studio
1 -
Business Architecture
1 -
Business Communication Services
1 -
Business Continuity
1 -
Business Data Fabric
3 -
Business Partner
12 -
Business Partner Master Data
10 -
Business Technology Platform
2 -
Business Trends
1 -
CA
1 -
calculation view
1 -
CAP
3 -
Capgemini
1 -
CAPM
1 -
Catalyst for Efficiency: Revolutionizing SAP Integration Suite with Artificial Intelligence (AI) and
1 -
CCMS
2 -
CDQ
12 -
CDS
2 -
Cental Finance
1 -
Certificates
1 -
CFL
1 -
Change Management
1 -
chatbot
1 -
chatgpt
3 -
CL_SALV_TABLE
2 -
Class Runner
1 -
Classrunner
1 -
Cloud ALM Monitoring
1 -
Cloud ALM Operations
1 -
cloud connector
1 -
Cloud Extensibility
1 -
Cloud Foundry
4 -
Cloud Integration
6 -
Cloud Platform Integration
2 -
cloudalm
1 -
communication
1 -
Compensation Information Management
1 -
Compensation Management
1 -
Compliance
1 -
Compound Employee API
1 -
Configuration
1 -
Connectors
1 -
Consolidation Extension for SAP Analytics Cloud
1 -
Controller-Service-Repository pattern
1 -
Conversion
1 -
Cosine similarity
1 -
cryptocurrency
1 -
CSI
1 -
ctms
1 -
Custom chatbot
3 -
Custom Destination Service
1 -
custom fields
1 -
Customer Experience
1 -
Customer Journey
1 -
Customizing
1 -
cyber security
2 -
Data
1 -
Data & Analytics
1 -
Data Aging
1 -
Data Analytics
2 -
Data and Analytics (DA)
1 -
Data Archiving
1 -
Data Back-up
1 -
Data Governance
5 -
Data Integration
2 -
Data Quality
12 -
Data Quality Management
12 -
Data Synchronization
1 -
data transfer
1 -
Data Unleashed
1 -
Data Value
8 -
database tables
1 -
Datasphere
2 -
datenbanksicherung
1 -
dba cockpit
1 -
dbacockpit
1 -
Debugging
2 -
Delimiting Pay Components
1 -
Delta Integrations
1 -
Destination
3 -
Destination Service
1 -
Developer extensibility
1 -
Developing with SAP Integration Suite
1 -
Devops
1 -
digital transformation
1 -
Documentation
1 -
Dot Product
1 -
DQM
1 -
dump database
1 -
dump transaction
1 -
e-Invoice
1 -
E4H Conversion
1 -
Eclipse ADT ABAP Development Tools
2 -
edoc
1 -
edocument
1 -
ELA
1 -
Embedded Consolidation
1 -
Embedding
1 -
Embeddings
1 -
Employee Central
1 -
Employee Central Payroll
1 -
Employee Central Time Off
1 -
Employee Information
1 -
Employee Rehires
1 -
Enable Now
1 -
Enable now manager
1 -
endpoint
1 -
Enhancement Request
1 -
Enterprise Architecture
1 -
ETL Business Analytics with SAP Signavio
1 -
Euclidean distance
1 -
Event Dates
1 -
Event Driven Architecture
1 -
Event Mesh
2 -
Event Reason
1 -
EventBasedIntegration
1 -
EWM
1 -
EWM Outbound configuration
1 -
EWM-TM-Integration
1 -
Existing Event Changes
1 -
Expand
1 -
Expert
2 -
Expert Insights
1 -
Fiori
14 -
Fiori Elements
2 -
Fiori SAPUI5
12 -
Flask
1 -
Full Stack
8 -
Funds Management
1 -
General
1 -
Generative AI
1 -
Getting Started
1 -
GitHub
8 -
Grants Management
1 -
groovy
1 -
GTP
1 -
HANA
5 -
HANA Cloud
2 -
Hana Cloud Database Integration
2 -
HANA DB
1 -
HANA XS Advanced
1 -
Historical Events
1 -
home labs
1 -
HowTo
1 -
HR Data Management
1 -
html5
8 -
HTML5 Application
1 -
Identity cards validation
1 -
idm
1 -
Implementation
1 -
input parameter
1 -
instant payments
1 -
Integration
3 -
Integration Advisor
1 -
Integration Architecture
1 -
Integration Center
1 -
Integration Suite
1 -
intelligent enterprise
1 -
Java
1 -
job
1 -
Job Information Changes
1 -
Job-Related Events
1 -
Job_Event_Information
1 -
joule
4 -
Journal Entries
1 -
Just Ask
1 -
Kerberos for ABAP
8 -
Kerberos for JAVA
8 -
Launch Wizard
1 -
Learning Content
2 -
Life at SAP
1 -
lightning
1 -
Linear Regression SAP HANA Cloud
1 -
local tax regulations
1 -
LP
1 -
Machine Learning
2 -
Marketing
1 -
Master Data
3 -
Master Data Management
14 -
Maxdb
2 -
MDG
1 -
MDGM
1 -
MDM
1 -
Message box.
1 -
Messages on RF Device
1 -
Microservices Architecture
1 -
Microsoft Universal Print
1 -
Middleware Solutions
1 -
Migration
5 -
ML Model Development
1 -
Modeling in SAP HANA Cloud
8 -
Monitoring
3 -
MTA
1 -
Multi-Record Scenarios
1 -
Multiple Event Triggers
1 -
Neo
1 -
New Event Creation
1 -
New Feature
1 -
Newcomer
1 -
NodeJS
2 -
ODATA
2 -
OData APIs
1 -
odatav2
1 -
ODATAV4
1 -
ODBC
1 -
ODBC Connection
1 -
Onpremise
1 -
open source
2 -
OpenAI API
1 -
Oracle
1 -
PaPM
1 -
PaPM Dynamic Data Copy through Writer function
1 -
PaPM Remote Call
1 -
PAS-C01
1 -
Pay Component Management
1 -
PGP
1 -
Pickle
1 -
PLANNING ARCHITECTURE
1 -
Popup in Sap analytical cloud
1 -
PostgrSQL
1 -
POSTMAN
1 -
Process Automation
2 -
Product Updates
4 -
PSM
1 -
Public Cloud
1 -
Python
4 -
Qlik
1 -
Qualtrics
1 -
RAP
3 -
RAP BO
2 -
Record Deletion
1 -
Recovery
1 -
recurring payments
1 -
redeply
1 -
Release
1 -
Remote Consumption Model
1 -
Replication Flows
1 -
Research
1 -
Resilience
1 -
REST
1 -
REST API
1 -
Retagging Required
1 -
Risk
1 -
Rolling Kernel Switch
1 -
route
1 -
rules
1 -
S4 HANA
1 -
S4 HANA Cloud
1 -
S4 HANA On-Premise
1 -
S4HANA
3 -
S4HANA_OP_2023
2 -
SAC
10 -
SAC PLANNING
9 -
SAP
4 -
SAP ABAP
1 -
SAP Advanced Event Mesh
1 -
SAP AI Core
8 -
SAP AI Launchpad
8 -
SAP Analytic Cloud Compass
1 -
Sap Analytical Cloud
1 -
SAP Analytics Cloud
4 -
SAP Analytics Cloud for Consolidation
2 -
SAP Analytics Cloud Story
1 -
SAP analytics clouds
1 -
SAP BAS
1 -
SAP Basis
6 -
SAP BODS
1 -
SAP BODS certification.
1 -
SAP BTP
20 -
SAP BTP Build Work Zone
2 -
SAP BTP Cloud Foundry
5 -
SAP BTP Costing
1 -
SAP BTP CTMS
1 -
SAP BTP Innovation
1 -
SAP BTP Migration Tool
1 -
SAP BTP SDK IOS
1 -
SAP Build
11 -
SAP Build App
1 -
SAP Build apps
1 -
SAP Build CodeJam
1 -
SAP Build Process Automation
3 -
SAP Build work zone
10 -
SAP Business Objects Platform
1 -
SAP Business Technology
2 -
SAP Business Technology Platform (XP)
1 -
sap bw
1 -
SAP CAP
2 -
SAP CDC
1 -
SAP CDP
1 -
SAP CDS VIEW
1 -
SAP Certification
1 -
SAP Cloud ALM
4 -
SAP Cloud Application Programming Model
1 -
SAP Cloud Integration for Data Services
1 -
SAP cloud platform
8 -
SAP Companion
1 -
SAP CPI
3 -
SAP CPI (Cloud Platform Integration)
2 -
SAP CPI Discover tab
1 -
sap credential store
1 -
SAP Customer Data Cloud
1 -
SAP Customer Data Platform
1 -
SAP Data Intelligence
1 -
SAP Data Migration in Retail Industry
1 -
SAP Data Services
1 -
SAP DATABASE
1 -
SAP Dataspher to Non SAP BI tools
1 -
SAP Datasphere
9 -
SAP DRC
1 -
SAP EWM
1 -
SAP Fiori
2 -
SAP Fiori App Embedding
1 -
Sap Fiori Extension Project Using BAS
1 -
SAP GRC
1 -
SAP HANA
1 -
SAP HCM (Human Capital Management)
1 -
SAP HR Solutions
1 -
SAP IDM
1 -
SAP Integration Suite
9 -
SAP Integrations
4 -
SAP iRPA
2 -
SAP Learning Class
1 -
SAP Learning Hub
1 -
SAP Odata
2 -
SAP on Azure
1 -
SAP PartnerEdge
1 -
sap partners
1 -
SAP Password Reset
1 -
SAP PO Migration
1 -
SAP Prepackaged Content
1 -
SAP Process Automation
2 -
SAP Process Integration
2 -
SAP Process Orchestration
1 -
SAP S4HANA
2 -
SAP S4HANA Cloud
1 -
SAP S4HANA Cloud for Finance
1 -
SAP S4HANA Cloud private edition
1 -
SAP Sandbox
1 -
SAP STMS
1 -
SAP SuccessFactors
2 -
SAP SuccessFactors HXM Core
1 -
SAP Time
1 -
SAP TM
2 -
SAP Trading Partner Management
1 -
SAP UI5
1 -
SAP Upgrade
1 -
SAP Utilities
1 -
SAP-GUI
8 -
SAP_COM_0276
1 -
SAPBTP
1 -
SAPCPI
1 -
SAPEWM
1 -
sapmentors
1 -
saponaws
2 -
SAPS4HANA
1 -
SAPUI5
4 -
schedule
1 -
Secure Login Client Setup
8 -
security
9 -
Selenium Testing
1 -
SEN
1 -
SEN Manager
1 -
service
1 -
SET_CELL_TYPE
1 -
SET_CELL_TYPE_COLUMN
1 -
SFTP scenario
2 -
Simplex
1 -
Single Sign On
8 -
Singlesource
1 -
SKLearn
1 -
soap
1 -
Software Development
1 -
SOLMAN
1 -
solman 7.2
2 -
Solution Manager
3 -
sp_dumpdb
1 -
sp_dumptrans
1 -
SQL
1 -
sql script
1 -
SSL
8 -
SSO
8 -
Substring function
1 -
SuccessFactors
1 -
SuccessFactors Time Tracking
1 -
Sybase
1 -
system copy method
1 -
System owner
1 -
Table splitting
1 -
Tax Integration
1 -
Technical article
1 -
Technical articles
1 -
Technology Updates
1 -
Technology Updates
1 -
Technology_Updates
1 -
Threats
1 -
Time Collectors
1 -
Time Off
2 -
Tips and tricks
2 -
Tools
1 -
Trainings & Certifications
1 -
Transport in SAP BODS
1 -
Transport Management
1 -
TypeScript
2 -
unbind
1 -
Unified Customer Profile
1 -
UPB
1 -
Use of Parameters for Data Copy in PaPM
1 -
User Unlock
1 -
VA02
1 -
Validations
1 -
Vector Database
1 -
Vector Engine
1 -
Visual Studio Code
1 -
VSCode
1 -
Web SDK
1 -
work zone
1 -
workload
1 -
xsa
1 -
XSA Refresh
1
- « Previous
- Next »
- Kyma Integration with SAP Cloud Logging. Part 2: Let's ship some traces in Technology Blogs by SAP
- Unveiling Customer Needs: SAP Signavio Community supporting our customer`s adoption in Technology Blogs by SAP
- Demystifying Transformers and Embeddings: Some GenAI Concepts in Technology Blogs by SAP
- Part 3 – SAP MDG – A Stepping Stone for SAP S/4HANA Journey in Technology Blogs by Members
- Kyma Integration with SAP Cloud Logging. Part 1: Introduction and shipping Logs in Technology Blogs by SAP
| User | Count |
|---|---|
| 11 | |
| 10 | |
| 7 | |
| 6 | |
| 4 | |
| 4 | |
| 3 | |
| 3 | |
| 3 | |
| 3 |
